Bài 1.53 trang 21 SBT Giải tích 12 Nâng cao

LG a

Khảo sát sự biến thiên và vẽ đồ thị (H) của hàm số

\(y = {{2x + 1} \over {x + 1}}\)

Lời giải chi tiết:

+) TXĐ: \(D = \mathbb{R}\backslash \left\{ { - 1} \right\}\)

+) Chiều biến thiên:

\(y' = \frac{{2 - 1}}{{{{\left( {x + 1} \right)}^2}}} = \frac{1}{{{{\left( {x + 1} \right)}^2}}} > 0,\) \(\forall x \in D\)

Hàm số đồng biến trên mỗi khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( { - 1; + \infty } \right)\).

\(\mathop {\lim }\limits_{x \to  \pm \infty } y = 2\) nên TCN: \(y = 2\)

\(\mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ + }} y =  - \infty ,\mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ - }} y =  + \infty \) nên TCĐ: \(x =  - 1\).

BBT:

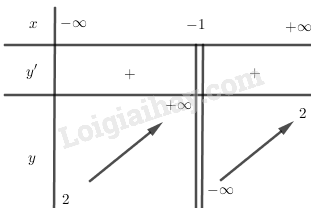
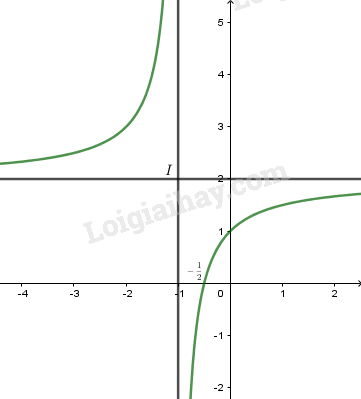
+) Đồ thị:

Cắt trục hoành tại \(\left( { - \frac{1}{2};0} \right)\), cắt trục tung tại \(\left( {0;1} \right)\).

LG b

Chứng minh rằng (H) nhận giao điểm I của hai đường tiệm cận của đồ thị làm tâm đối xứng.

Lời giải chi tiết:

Công thức chuyển hệ tọa độ theo véc tơ \(\overrightarrow {OI} \) là: \(\left\{ \begin{array}{l}x = X - 1\\y = Y + 2\end{array} \right.\)

Phương trình đường cong trong hệ tọa độ IXY là:

\(\begin{array}{l}Y + 2 = \frac{{2\left( {X - 1} \right) + 1}}{{X - 1 + 2}}\\ \Leftrightarrow Y + 2 = \frac{{2X - 1}}{X}\\ \Leftrightarrow Y + 2 = 2 - \frac{1}{X}\\ \Leftrightarrow Y =  - \frac{1}{X}\end{array}\)

Đây là hàm số lẻ nên đồ thị nhận I làm tâm đối xứng.