Đề kiểm tra 15 phút - Chương 2 - Đề số 3 - Đại số 10

Đề bài

Câu 1. Chúng minh hàm số  đồng biến trên các khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( { - 1; + \infty } \right)\) .

Câu 2. Xét tính chẵn – lẻ của hàm số \(f(x) = \dfrac{{\sqrt {5 + 2x}  - \sqrt {5 - 2x} }}{x}\)

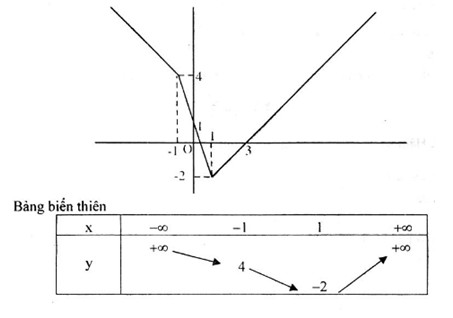
Câu 3. Vẽ đồ thị và lập bẳng biến thiên của hàm số \(y = 2\left| {x - 1} \right| - \left| {x + 1} \right|\)

Lời giải chi tiết

Câu 1. Hàm số \(y = \dfrac{{2x - 1}}{{x + 1}}\) có tập xác định \(D = \mathbb{R}\backslash \left\{ { - 1} \right\}\) .

Lấy \({x_1},{x_2} \in D,{x_1} \ne {x_2}\) .

Lập tỉ số

\(\begin{array}{l}k = \dfrac{{f\left( {{x_1}} \right) - f\left( {{x_2}} \right)}}{{{x_2} - {x_1}}}\\\;\; = \dfrac{{\dfrac{{2{x_2} - 1}}{{{x_2} + 1}} - \dfrac{{2{x_1} - 1}}{{{x_1} + 1}}}}{{{x_2} - {x_1}}}\\\;\; = \dfrac{{\left( {2{x_2} - 1} \right)\left( {{x_1} + 1} \right) - \left( {2{x_1} - 1} \right)\left( {{x_2} + 1} \right)}}{{\left( {{x_2} - {x_1}} \right)\left( {{x_1} + 1} \right)\left( {{x_2} + 1} \right)}}\end{array}\)

\(\begin{array}{l}\;\; = \dfrac{{3{x_2} - 3{x_1}}}{{\left( {{x_2} - {x_1}} \right)\left( {{x_1} + 1} \right)\left( {{x_2} + 1} \right)}}\\ \;\;= \dfrac{3}{{\left( {{x_1} + 1} \right)\left( {{x_2} + 1} \right)}}\end{array}\)

Nếu \({x_1},{x_2} \in \left( { - \infty ; - 1} \right)\) thì \({x_1} <  - 1,{x_2} <  - 1\) .Suy ra \({x_1} + 1 < 0,{x_2} + 1 < 0\) . Do đó k > 0. Vậy hàm số đồng biến trên khoảng \(\left( { - \infty ; - 1} \right)\) .

Nếu \({x_1},{x_2} \in \left( { - 1; + \infty } \right)\) thì \({x_1} >  - 1,{x_2} >  - 1\). Suy ra \({x_1} + 1 > 0,{x_2} + 1 > 0\) . Do đó k > 0. Vây hàm số đồng biến trên khoảng \(\left( { - 1; + \infty } \right)\)

Câu 2. Hàm số \(f(x) = \dfrac{{\sqrt {5 + 2x}  - \sqrt {5 - 2x} }}{x}\) được xác định khi và chỉ khi

\(\left\{ \begin{array}{l}5 + 2x \ge 0\\5 - 2x \ge 0\\x \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge  - \dfrac{5}{2}\\x \le \dfrac{5}{2}\\x \ne 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l} - \dfrac{5}{2} \le x \le \dfrac{5}{2}\\x \ne 0\end{array} \right.\)

Vậy hàm số có tập xác định \(D = \left[ { - \dfrac{5}{2};0} \right) \cup \left( {0;\dfrac{5}{2}} \right]\) .

Với mọi \(x \in D\) ta có

\( - x \in D\)

\(\begin{array}{l}f\left( { - x} \right) = \dfrac{{\sqrt {5 - 2x}  - \sqrt {5 + 2x} }}{{ - x}}\\{\rm{         }} = \dfrac{{\sqrt {5 + 2x}  - \sqrt {5 - 2x} }}{x} = f(x)\end{array}\)

Vậy hàm số \(f(x) = \dfrac{{\sqrt {5 + 2x}  - \sqrt {5 - 2x} }}{x}\) là hàm số chẵn.

Câu 3.

Ta có:

\(y = \left\{ \begin{array}{l}2\left( { - x + 1} \right) - \left( { - x - 1} \right){\rm{\; khi\; x <  - 1}}\\{\rm{2}}\left( { - x + 1} \right) - \left( {x + 1} \right){\rm{   khi - 1}} \le {\rm{x}} \le {\rm{1}}\\{\rm{2}}\left( {x - 1} \right) - \left( {x + 1} \right){\rm{     khi x > 1}}\end{array} \right.\\\;\; = \left\{ \begin{array}{l} - x + 3{\rm{  khi x <  - 1}}\\{\rm{ - 3x + 1   khi  - 1}} \le {\rm{x}} \le {\rm{1}}\\{\rm{x - 3       khi x > 1}}\end{array} \right.\)

Đồ thị