Bài 70 trang 154 SGK Đại số 10 nâng cao
Giải các bất phương trình sau:
Giải các bất phương trình sau:
LG a
|x2 – 5x + 4| ≤ x2 + 6x + 5
Phương pháp giải:
Áp dụng:
\(\left| f \right| \le g \Leftrightarrow \left\{ \begin{array}{l}
g \ge 0\\
- g \le f \le g
\end{array} \right.\)
Lời giải chi tiết:
\(\begin{array}{l}
\left| {{x^2} - 5x + 4} \right| \le {x^2} + 6x + 5\\
\Leftrightarrow \left\{ \begin{array}{l}
{x^2} + 6x + 5 \ge 0\\
- {x^2} - 6x - 5 \le {x^2} - 5x + 4 \le {x^2} + 6x + 5
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
{x^2} + 6x + 5 \ge 0\\
- {x^2} - 6x - 5 \le {x^2} - 5x + 4\\
{x^2} - 5x + 4 \le {x^2} + 6x + 5
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
\left[ \begin{array}{l}
x \ge - 1\\
x \le - 5
\end{array} \right.\\
- 2{x^2} - x - 9 \le 0\left( {dung} \right)\\
- 11x - 1 \le 0
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
\left[ \begin{array}{l}
x \ge - 1\\
x \le - 5
\end{array} \right.\\
x \ge - \frac{1}{{11}}
\end{array} \right.\\
\Leftrightarrow x \ge - \frac{1}{{11}}
\end{array}\)
Vậy tập nghiệm của bpt là \(S = \left[ { - \frac{1}{{11}}; + \infty } \right)\).
Cách khác:
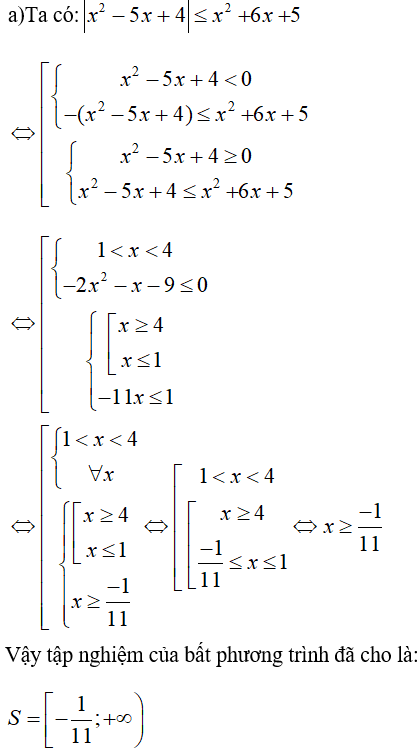
LG b
4x2 + 4x - |2x + 1| ≥ 5
Phương pháp giải:
Áp dụng:
\(\left| f \right| \le g \Leftrightarrow \left\{ \begin{array}{l}
g \ge 0\\
- g \le f \le g
\end{array} \right.\)
Lời giải chi tiết:
\(\begin{array}{l}
\Leftrightarrow \left\{ \begin{array}{l}
4{x^2} + 4x - 5 \ge 0\\
- 4{x^2} - 4x + 5 \le 2x + 1 \le 4{x^2} + 4x - 5
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
4{x^2} + 4x - 5 \ge 0\\
- 4{x^2} - 4x + 5 \le 2x + 1\\
2x + 1 \le 4{x^2} + 4x - 5
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
4{x^2} + 4x - 5 \ge 0\\
- 4{x^2} - 6x + 4 \le 0\\
- 4{x^2} - 2x + 6 \le 0
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
\left[ \begin{array}{l}
x \ge \frac{{ - 1 + \sqrt 6 }}{2}\\
x \le \frac{{ - 1 - \sqrt 6 }}{2}
\end{array} \right.\\
\left[ \begin{array}{l}
x \ge \frac{1}{2}\\
x \le - 2
\end{array} \right.\\
\left[ \begin{array}{l}
x \ge 1\\
x \le - \frac{3}{2}
\end{array} \right.
\end{array} \right.\\
\Leftrightarrow \left[ \begin{array}{l}
x \ge 1\\
x \le - 2
\end{array} \right.
\end{array}\)
Vậy \(S = (-∞, -2] ∪ [1, + ∞)\).
Cách khác:
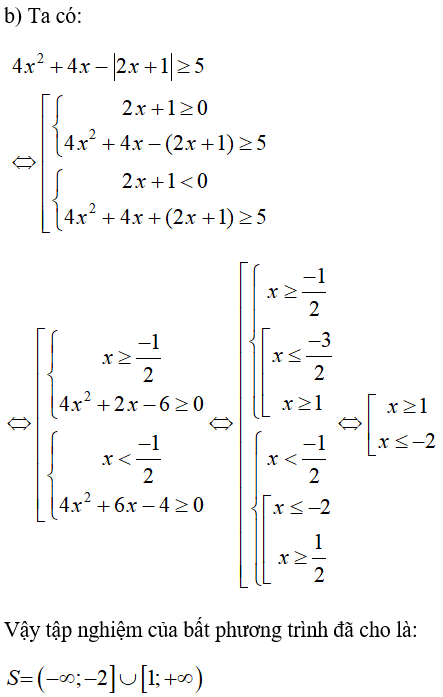
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 70 trang 154 SGK Đại số 10 nâng cao timdapan.com"







