Bài 64 trang 146 SGK Đại số 10 nâng cao

Đề bài

Tìm các giá trị của m để hệ bất phương trình sau có nghiệm:

\(\left\{ \matrix{
{x^2} + 2x - 15 < 0 \hfill \cr 
(m + 1)x \ge 3 \hfill \cr} \right.\)

Lời giải chi tiết

Ta có: x² + 2x – 15 < 0 ⇔ -5 < x < 3 \( \Rightarrow {S_1} = \left( { - 5;3} \right)\)

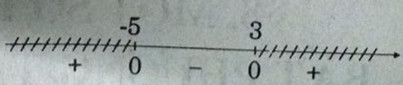
Ta xét bất phương trình: (m + 1)x ≥ 3  (*)

+ Nếu m = -1 thì \(\left( * \right) \Leftrightarrow 0x \ge 3\) (vô lí) \(\Rightarrow  S_2 = Ø\)

Do đó \({S_1} \cap {S_2} = \emptyset \) (loại)

+ Nếu m > -1 thì: \((*) \Leftrightarrow x \ge {3 \over {m + 1}}\)

\( \Rightarrow {S_2} = \left[ {\frac{3}{{m + 1}}; + \infty } \right)\)

Hệ có nghiệm: \( \Leftrightarrow {S_1} \cap {S_2} \ne \emptyset \)

\(\begin{array}{l}
\Leftrightarrow \frac{3}{{m + 1}} < 3 \Leftrightarrow 3 < 3\left( {m + 1} \right)\\
\left( {do\,m > - 1} \right)\\
\Leftrightarrow 3m > 0 \Leftrightarrow m > 0
\end{array}\)

Kết hợp \(m>-1\) ta được \(m>0\).

+ Nếu m < -1 thì \((*) \Leftrightarrow x \le {3 \over {m + 1}}\) \( \Rightarrow {S_2} = \left( { - \infty ;\frac{3}{{m + 1}}} \right]\)

Hệ có nghiệm: \( \Leftrightarrow {S_1} \cap {S_2} \ne \emptyset \)

\(\begin{array}{l}
\Leftrightarrow \frac{3}{{m + 1}} > - 5 \Leftrightarrow 3 < - 5\left( {m + 1} \right)\\
\left( {do\,m < - 1 \Rightarrow m + 1 < 0} \right)\\
\Leftrightarrow 5m + 8 < 0 \Leftrightarrow m < - \frac{8}{5}
\end{array}\)

Kết hợp \(m < -1 \) ta được \(m < - \frac{8}{5}\).

Vậy hệ có nghiệm khi và chỉ khi: 

\(\left[ \matrix{
m < - {8 \over 5} \hfill \cr 
m > 0 \hfill \cr} \right.\)