Bài 62 trang 146 SGK Đại số 10 nâng cao

Giải các hệ bất phương trình

LG a.

\(\left\{ \matrix{
4x - 3 < 3x + 4 \hfill \cr 
{x^2} - 7x + 10 \le 0 \hfill \cr} \right.\)

Phương pháp giải:

Giải từng bpt trong hệ và kết luận nghiệm.

Lời giải chi tiết:

Ta có: 

\( \Leftrightarrow \left\{ \matrix{
4x - 3 < 3x + 4 \hfill \cr 
{x^2} - 7x + 10 \le 0 \hfill \cr} \right. \) \(\Leftrightarrow \left\{ \matrix{
x < 7 \hfill \cr 
2 \le x \le 5 \hfill \cr} \right.\)

\(\Leftrightarrow 2 \le x \le 5\)

Vậy \(S = [2, 5]\)

LG b.

\(\left\{ \matrix{
2{x^2} + 9x - 7 > 0 \hfill \cr 
{x^2} + x - 6 \le 0 \hfill \cr} \right.\)

Lời giải chi tiết:

Ta có:

\(\eqalign{
& \left\{ \matrix{
2{x^2} + 9x - 7 > 0 \hfill \cr 
{x^2} + x - 6 \le 0 \hfill \cr} \right.\cr & \Leftrightarrow \left\{ \matrix{
\left[ \matrix{
x < {{ - 9 - \sqrt {137} } \over 4} \hfill \cr 
x > {{ - 9 + \sqrt {137} } \over 4} \hfill \cr} \right. \hfill \cr 
- 3 \le x \le 2 \hfill \cr} \right. \cr 
& \Leftrightarrow {{ - 9 + \sqrt {137} } \over 4} < x \le 2 \cr} \) 

Vậy \(S = ({{ - 9 + \sqrt {137} } \over 4};2{\rm{]}}\)

LG c.

\(\left\{ \matrix{
{x^2} - 9 < 0 \hfill \cr 
(x - 1)(3{x^2} + 7x + 4) \ge 0 \hfill \cr} \right.\)

Lời giải chi tiết:

Ta có:

\({x^2} - 9 < 0 \Leftrightarrow  - 3 < x < 3\).

Giải bpt \((x - 1)(3{x^2} + 7x + 4) \ge 0\) bằng cách xét dấu ta có bảng:

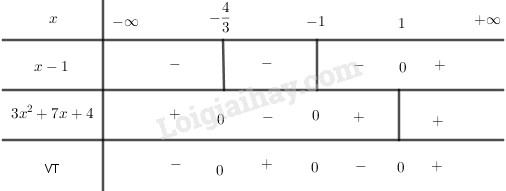
\( \Rightarrow \left( {x - 1} \right)\left( {3{x^2} + 7x + 4} \right) \ge 0\) \( \Leftrightarrow \left[ \begin{array}{l}
- \frac{4}{3} \le x \le - 1\\
x \ge 1
\end{array} \right.\)

Do đó:

\(\eqalign{
& \left\{ \matrix{
{x^2} - 9 < 0 \hfill \cr 
(x - 1)(3{x^2} + 7x + 4) \ge 0 \hfill \cr} \right.\cr& \Leftrightarrow \left\{ \matrix{
- 3 < x < 3 \hfill \cr 
\left[ \matrix{
- {4 \over 3} \le x \le - 1 \hfill \cr 
x \ge 1 \hfill \cr} \right. \hfill \cr} \right. \cr 
& \Leftrightarrow \left[ \matrix{
- {4 \over 3} \le x \le - 1 \hfill \cr 
1 \le x < 3 \hfill \cr} \right. \cr} \)

Vậy \(S = \,{\rm{[}} - {4 \over 3},\, - 1{\rm{]}}\, \cup {\rm{[}}1,\,3)\)