Bài 60 trang 146 SGK Đại số 10 nâng cao

Giải các bất phương trình sau:

LG a.

\({{{x^4} - {x^2}} \over {{x^2} + 5x + 6}} \le 0\)

Phương pháp giải:

Lập bảng xét dấu suy ra tập nghiệm của bpt.

Lời giải chi tiết:

Ta có:

\({{{x^4} - {x^2}} \over {{x^2} + 5x + 6}} \le 0 \) \(\Leftrightarrow {{{x^2}({x^2} - 1)} \over {{x^2} + 5x + 6}} \le 0\)

\(\begin{array}{l}
{x^2} = 0 \Leftrightarrow x = 0\\
{x^2} - 1 = 0 \Leftrightarrow x = \pm 1\\
{x^2} + 5x + 6 = 0 \Leftrightarrow \left[ \begin{array}{l}
x = - 2\\
x = - 3
\end{array} \right.
\end{array}\)

Bảng xét dấu:

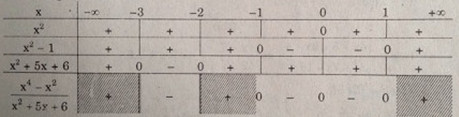
Vậy \(S = (-3, -2) ∪ [-1, 1]\)

LG b.

\({1 \over {{x^2} - 5x + 4}} < {1 \over {{x^2} - 7x + 10}}\)

Lời giải chi tiết:

Ta có:

\(\eqalign{
& {1 \over {{x^2} - 5x + 4}} < {1 \over {{x^2} - 7x + 10}} \cr&\Leftrightarrow {1 \over {{x^2} - 5x + 4}} - {1 \over {{x^2} - 7x + 10}} < 0 \cr 
&  \Leftrightarrow \frac{{{x^2} - 7x + 10 - \left( {{x^2} - 5x + 4} \right)}}{{\left( {{x^2} - 5x + 4} \right)\left( {{x^2} - 7x + 10} \right)}} < 0\cr &\Leftrightarrow {{ - 2x + 6} \over {({x^2} - 5x + 4)({x^2} - 7x + 10)}} < 0 \cr} \)

Xét dấu vế trái:

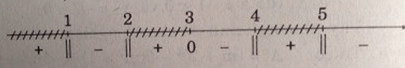
Vậy \(S = (1, 2) ∪ (3, 4) ∪ (5, +∞)\).