Bài 53 trang 145 SGK Đại số 10 nâng cao

Giải các bất phương trình

LG a

-5x² + 4x + 12 < 0

Phương pháp giải:

Xét dấu vế trái, từ đó suy ra tập nghiệm của bpt.

Lời giải chi tiết:

Ta có:

\( - 5{x^2} + 4x + 12 = 0 \Leftrightarrow \left[ \matrix{
x = - {6 \over 5} \hfill \cr 
x = 2 \hfill \cr} \right.\)

Có a = -5 < 0 nên:

Bảng xét dấu:

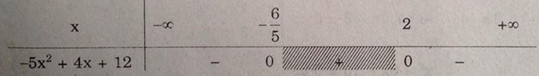Do đó, -5x² + 4x + 12 < 0 khi

\(\left[ \begin{array}{l}
x < - \frac{6}{5}\\
x > 2
\end{array} \right.\)

Tập nghiệm của bất phương trình \(S = ( - \infty , - {6 \over 5}) \cup (2, + \infty )\)

LG b

16x² + 40x +25 < 0

Lời giải chi tiết:

Ta có: \(16{x^2} + 40x + 25 = 0 \) \(\Leftrightarrow x =  - {5 \over 4}\) (nghiệm kép)

\(\eqalign{
& a = 16 > 0 \cr 
& \Delta ' = 200 - 16.25 = 0 \cr 
& \Rightarrow 16{x^2} + 40x + 25 \ge 0\,\,\forall x \in R \cr} \)

Nên không có giá trị nào của x để 16x² + 40x +25 < 0.

Vậy S = Ø.

Cách khác:

\(16{x^2} + 40x + 25\) \( = {\left( {4x} \right)^2} + 2.\left( {4x} \right).5 + {5^2} \) \( = {\left( {4x + 5} \right)^2} \ge 0,\forall x\)

Nên không có giá trị nào của x để 16x² + 40x +25 < 0.

Vậy S = Ø.

LG c

3x² - 4x + 4 ≥ 0

Lời giải chi tiết:

Ta có:

a = 3

Δ’ = 4 – 12 = -8 < 0

⇒ 3x² - 4x + 4 > 0 ∀x ∈ R

Nên với mọi x ta đều có 3x² - 4x + 4 ≥ 0.

Vậy S = R

LG d

 x² - x - 6 ≤ 0

Lời giải chi tiết:

Ta có:

\({x^2} - x - 6 = 0 \) \(\Leftrightarrow \left[ \matrix{
x = 3 \hfill \cr 
x = - 2 \hfill \cr} \right.\)

Có a = 1 > 0 nên bảng xét dấu:

Do đó, \({x^2} - x - 6 \le 0 \Leftrightarrow  - 2 \le x \le 3\) nên tập nghiệm S = [-2, 3]