Bài 63 trang 102 SGK Đại số 10 nâng cao
Tìm a, b và c để Parabol y = ax2 + bx + c có đỉnh là 1(1; -4) và đi qua điểm M(2; -3). Hãy vẽ Parabol nhận được.
Đề bài
Tìm a, b và c để Parabol y = ax2 + bx + c có đỉnh là I(1; -4) và đi qua điểm M(2; -3). Hãy vẽ Parabol nhận được.
Phương pháp giải - Xem chi tiết
Sử dụng các kết quả sau:
Đỉnh của Parabol y = ax2 + bx + c là \((- {b \over {2a}};-{\Delta \over {4a}} )\)
\(A(x_0;y_0)\) thuộc Parabol khi và chỉ khi \(y_0 = ax^2_0 + bx_0 + c\)
Lời giải chi tiết
\(I(1, -4)\) là đỉnh của Parabol nên:
\(\left\{ \matrix{
- {b \over {2a}} = 1 \hfill \cr
- 4 = a + b + c \hfill \cr} \right.\)
\(M(2, -3)\) thuộc parabol nên: \(-3 = 4a + 2b + c\)
Ta có hệ:
\(\left\{ \matrix{
2a + b = 0 \hfill \cr
a + b + c = - 4 \hfill \cr
4a + 2b + c = - 3 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
a = 1 \hfill \cr
b = - 2 \hfill \cr
c = - 3 \hfill \cr} \right.\)
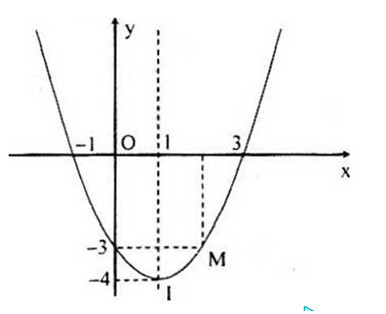
Vậy \(y = x^2 – 2x – 3\)
Đồ thị hàm số: \(y = x^2 – 2x – 3\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 63 trang 102 SGK Đại số 10 nâng cao timdapan.com"







