Bài 52 trang 101 SGK Đại số 10 nâng cao

Đề bài

Hệ phương trình dạng

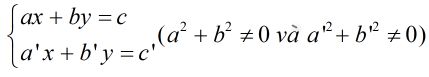
có thể có nghiệm trong trường hợp nào?

Áp dụng: Tìm a để hệ có phương trình

\(\left\{ \matrix{
ax + y = {a^2} \hfill \cr 
x + ay = 1 \hfill \cr} \right.\) có nghiệm?

Lời giải chi tiết

Hệ đã cho có nghiệm khi có nghiệm duy nhất hoặc có vô số nghiệm.

+ Hệ có nghiệm duy nhất khi D ≠ 0

+ Hệ vô số nghiệm khi D = D_x = D_y = 0

Vậy hệ đã cho có nghiệm khi D ≠ 0 hoặc D = D_x = D_y = 0.

Áp dụng:

Ta có:

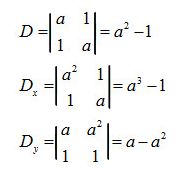
+ Nếu \(a ≠  ± 1\) hệ có nghiệm duy nhất

+ Nếu \(a = 1\) thì hệ có vô số nghiệm

+ Nếu \(a = -1\) thì hệ vô nghiệm (Do D_x = -2 ≠ 0)

Vậy hệ có nghiệm \(⇔ a ≠ -1\).

Cách trình bày khác:

Hệ có nghiệm duy nhất khi \(D \ne 0 \Leftrightarrow {a^2} - 1 \ne 0 \Leftrightarrow a \ne  \pm 1\)

Hệ vô số nghiệm khi

\(\begin{array}{l}D = {D_x} = {D_y} = 0\\ \Leftrightarrow \left\{ \begin{array}{l}{a^2} - 1 = 0\\{a^3} - 1 = 0\\a - {a^2} = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}\left( {a - 1} \right)\left( {a + 1} \right) = 0\\\left( {a - 1} \right)\left( {{a^2} + a + 1} \right) = 0\\a\left( {1 - a} \right) = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}a = 1\\a =  - 1\end{array} \right.\\a = 1\\\left[ \begin{array}{l}a = 0\\a = 1\end{array} \right.\end{array} \right. \Leftrightarrow a = 1\end{array}\)

Do đó với \(\left[ \begin{array}{l}a \ne \pm 1\\a = 1\end{array} \right. \Leftrightarrow a \ne - 1\) thì hệ có nghiệm.