Bài 61 trang 102 SGK Đại số 10 nâng cao

Giải và biện luận các hệ phương trình

LG a

\(\left\{ \matrix{
mx + 3y = m - 1 \hfill \cr 
2x + (m - 1)y = 3 \hfill \cr} \right.\)

Lời giải chi tiết:

Ta có:

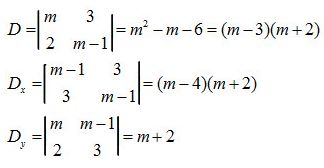
+) Nếu \(D \ne 0 \Leftrightarrow \left\{ \begin{array}{l}m \ne 3\\m \ne  - 2\end{array} \right.\) thì hệ có nghiệm \(\left\{ \begin{array}{l}x = \frac{{{D_x}}}{D} = \frac{{\left( {m - 4} \right)\left( {m + 2} \right)}}{{\left( {m - 3} \right)\left( {m + 2} \right)}} = \frac{{m - 4}}{{m - 3}}\\y = \frac{{{D_y}}}{D} = \frac{{m + 2}}{{\left( {m - 3} \right)\left( {m + 2} \right)}} = \frac{1}{{m - 3}}\end{array} \right.\)

+) Nếu \(D = 0 \Leftrightarrow \left[ \begin{array}{l}m = 3\\m =  - 2\end{array} \right.\)

- Với \(m = 3\): hệ vô nghiệm (do D_y = 5 ≠ 0)

- Với \(m = -2\) hệ thành 

\(\left\{ \matrix{
- 2x + 3y = - 3 \hfill \cr 
2x - 3y = 3 \hfill \cr} \right. \Leftrightarrow y = {1 \over 3}(2x - 3)\)

Hệ có vô số nghiệm.

LG b

\(\left\{ \matrix{
5x + (a - 2)y = a \hfill \cr 
(a + 3)x + (a + 3)y = 2a \hfill \cr} \right.\)

Lời giải chi tiết:

Ta có:

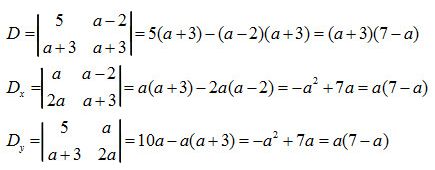
Nếu \(D \ne 0 \Leftrightarrow \left\{ \begin{array}{l}a \ne  - 3\\a \ne 7\end{array} \right.\) thì hệ có nghiệm \(\left\{ \begin{array}{l}x = \frac{{a\left( {7 - a} \right)}}{{\left( {a + 3} \right)\left( {7 - a} \right)}} = \frac{a}{{a + 3}}\\y = \frac{{a\left( {7 - a} \right)}}{{\left( {a + 3} \right)\left( {7 - a} \right)}} = \frac{a}{{a + 3}}\end{array} \right.\)

Nếu \(D = 0\) \( \Leftrightarrow \left[ \begin{array}{l}a =  - 3\\a = 7\end{array} \right.\)

+ Với \(a=-3\) thì hệ vô nghiệm vì \({D_x} =  - 30 \ne 0\)

+ Với \(a = 7\), hệ thành 

\(\left\{ \matrix{
5x + 5y = 7 \hfill \cr 
10x + 10y = 14 \hfill \cr} \right. \Leftrightarrow y = - x + {7 \over 5}\)

Hệ có vô số nghiệm \(\left( {x;{7 \over 5} - x} \right),\,x \in\mathbb R\)