Bài 5 trang 88 SGK Toán 11 tập 2 – Cánh Diều
Cho hình chóp O.ABC có \(\widehat {AOB} = \widehat {BOC} = \widehat {COA} = 90^\circ \). Chứng minh rằng:
Đề bài
Cho hình chóp O.ABC có \(\widehat {AOB} = \widehat {BOC} = \widehat {COA} = 90^\circ \). Chứng minh rằng:
a) \(BC \bot OA\)
b) \(CA \bot OB\)
c) \(AB \bot OC\)
Phương pháp giải - Xem chi tiết
Dựa vào định lí vừa học để chứng minh
Lời giải chi tiết
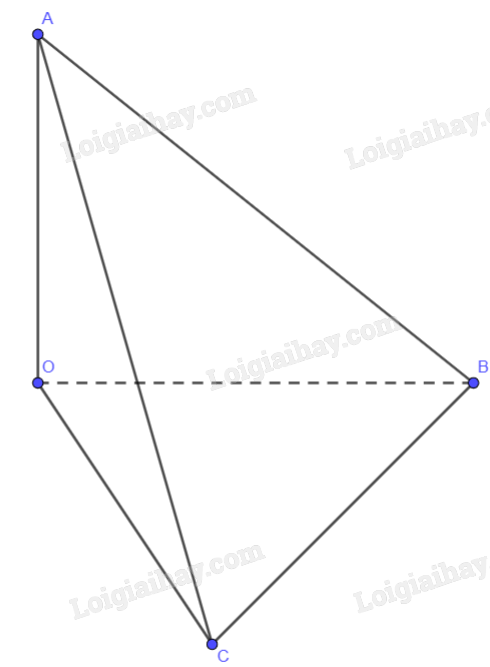
a) Ta có: \(\left. \begin{array}{l}OA \bot OB\\OA \bot OC\end{array} \right\} \Rightarrow OA \bot \left( {OBC} \right)\)
Mà \(BC \in \left( {OBC} \right) \Rightarrow OA \bot BC\)
b) Ta có \(\left. \begin{array}{l}OA \bot OB\\OB \bot OC\end{array} \right\} \Rightarrow OB \bot \left( {OAC} \right)\)
Mà \(CA \in \left( {OAC} \right) \Rightarrow CA \bot OB\)
c) Ta có \(\left. \begin{array}{l}OC \bot OB\\OA \bot OC\end{array} \right\} \Rightarrow OC \bot \left( {OAB} \right)\)
Mà \(AB \in \left( {OAB} \right) \Rightarrow AB \bot OC\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 5 trang 88 SGK Toán 11 tập 2 – Cánh Diều timdapan.com"







