Bài 4 trang 88 SGK Toán 11 tập 2 – Cánh Diều
Cho tứ diện ABCD có (AB bot (BCD),BC bot CD). Gọi M và N lần lượt là hình chiếu vuông góc của B trên AC và AD. Chứng minh rằng:
Đề bài
Cho tứ diện ABCD có \(AB \bot (BCD),BC \bot CD\). Gọi M và N lần lượt là hình chiếu vuông góc của B trên AC và AD. Chứng minh rằng:
a) \(CD \bot BM\)
b, \(BM \bot MN\)
Phương pháp giải - Xem chi tiết
Dựa vào quan hệ từ vuông góc đến song song trong không gian để chứng minh
Lời giải chi tiết
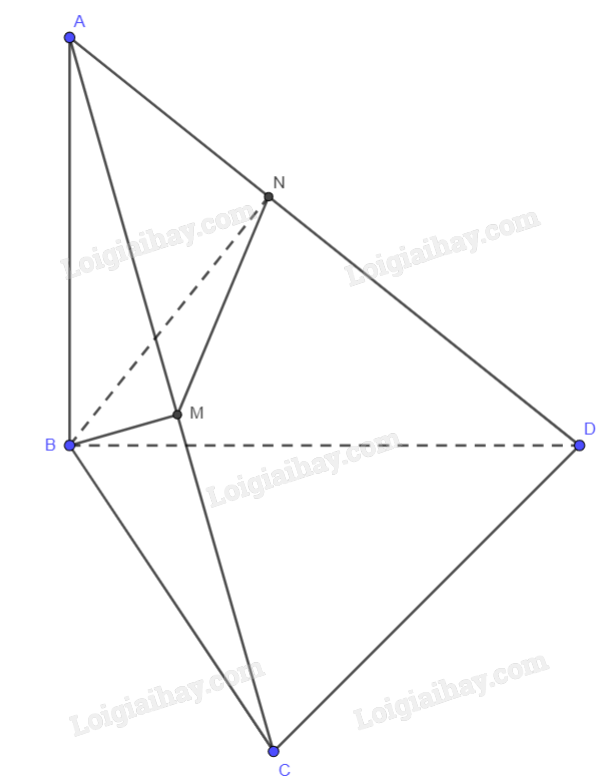
a) Vì \(AB \bot \left( {BCD} \right) \Rightarrow AB \bot CD\)
Mà \(CD \bot BC\)\( \Rightarrow CD \bot \left( {ABC} \right)\)
Lại có \(BM \in \left( {ABC} \right)\)\( \Rightarrow CD \bot BM\)
b) Ta có \(\left. \begin{array}{l}BM \bot CD\\BM \bot AC\end{array} \right\} \Rightarrow BM \bot \left( {ACD} \right)\)
Mà \(MN \in \left( {ACD} \right) \Rightarrow BM \bot MN\)
Mẹo Tìm đáp án nhanh nhất
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 4 trang 88 SGK Toán 11 tập 2 – Cánh Diều timdapan.com"
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 4 trang 88 SGK Toán 11 tập 2 – Cánh Diều timdapan.com"







