Bài 28 trang 58 SGK Toán 9 tập 1
Giải bài 28 trang 58 SGK Toán 9 tập 1. Cho hàm số y = -2x + 3.
Đề bài
Cho hàm số \(y = -2x + 3.\)
a) Vẽ đồ thị của hàm số.
b) Tính góc tạo bởi đường thẳng \(y = -2x + 3\) và trục \(Ox\) (làm tròn đến phút).
Phương pháp giải - Xem chi tiết
a) Cách vẽ đồ thị hàm số \(y=ax+b,\ (a \ne 0)\): Đồ thị hàm số \(y=ax+b \, \, (a\neq 0)\) là đường thẳng:
+) Cắt trục hoành tại điểm \(A(-\dfrac{b}{a}; \, 0).\)
+) Cắt trục tung tại điểm \(B(0;b).\)
Xác định tọa độ hai điểm \(A\) và \(B\) sau đó kẻ đường thẳng đi qua hai điểm đó ta được đồ thị hàm số \(y=ax+b \, \, (a\neq 0).\)
b) Góc tạo bởi đường thẳng \(y=a x+b \, \ (a \neq 0)\) là góc \(\alpha \) ta có: \(tan \alpha = a.\)
+) Với \(a<0\), góc \(\alpha\) là góc tù.
+) Với \(a>0\), góc \(\alpha\) là góc nhọn.
Sử dụng các công thức lượng giác để tính góc cần tìm: Cho tam giác \(ABC\) vuông tại \(A\). Khi đó: \(\tan B = \dfrac{AC}{AB}.\)
Lời giải chi tiết
a) Hàm số \(y = -2x + 3.\)
Cho \(x=0 \Rightarrow y=-2.0+3=0+3=3 \Rightarrow A(0; 3)\)
Cho \(y=0 \Rightarrow 0=-2.x+3 \Leftrightarrow x=\dfrac{3}{2} \Rightarrow B{\left(\dfrac{3}{2}; 0\right)}\)
Vẽ đường thẳng đi qua hai điểm \(A(0; 3)\) và \(B{\left(\dfrac{3}{2}; 0\right)}\) ta được đồ thị hàm số \(y = -2x + 3.\).
Đồ thị được vẽ như hình bên.
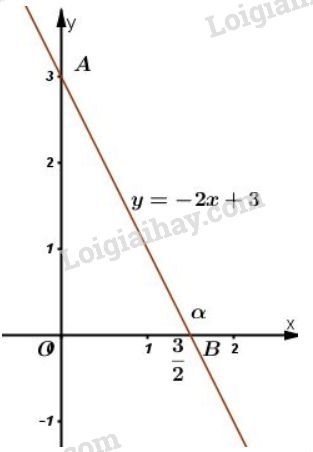
b) Gọi \(\alpha \) là góc giữa đường thẳng \(y = -2x + 3\) và trục \(Ox \Rightarrow \alpha = \widehat{ABx}\).
Xét tam giác vuông \(OAB\) vuông tại \(O\), ta có:
\(\tan \widehat {OBA} = \dfrac{OA}{OB} = \dfrac{3}{\dfrac{3}{2}}=2\)
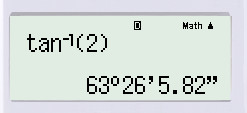
Thực hiện bấm máy tính, ta được:
\(\widehat {ABO} \approx {63^0}26'\)
Lại có \(\widehat {ABO}\) và \(\widehat {ABx}\) là hai góc kề bù, tức là:
\(\widehat {ABO} + \widehat {ABx} =180^0\)
\(\Leftrightarrow \widehat {ABx}=180^0 -\widehat {ABO} \)
\(\Leftrightarrow \widehat {ABx} \approx 180^0 -{63^0}26' \)
\(\Leftrightarrow \widehat {ABx} \approx 116^0 34'\)
Vậy \(\alpha \approx {116^0}34'\).
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 28 trang 58 SGK Toán 9 tập 1 timdapan.com"