Bài 2 trang 15 SGK Đại số 10

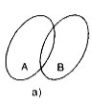
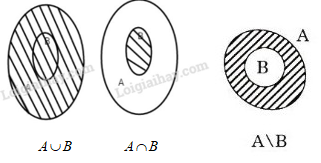
Vẽ lại và gạch chéo các tập hợp \(A ∩ B, A ∪ B, A\backslash B\) (h.9) trong các trường hợp sau.

LG a

Phương pháp giải:

1) Giao của hai tập hơp: Tập hợp C gồm các phần tử vừa thuộc A, vừa thuộc B được gọi là giao của A và B.

Kí hiệu: \(A \cap B\)

2) Hợp của hai tập hợp:  Tập hợp C gồm các phần tử thuộc A hoặc thuộc B được gọi là hợp của A và B.

Kí hiệu: \(A \cup B\)

3) Hiệu và phần bù của hai tập hợp:

Tập hợp C gồm các phần tử thuộc A nhưng không thuộc B gọi là hiệu của A và B.

Khi \(B \subset A\) thi A\B được gọi là phần bù của B trong A, kí hiệu \({C_A}B\)

Lời giải chi tiết:

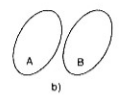
LG b

Phương pháp giải:

1) Giao của hai tập hơp: Tập hợp C gồm các phần tử vừa thuộc A, vừa thuộc B được gọi là giao của A và B.

Kí hiệu: \(A \cap B\)

2) Hợp của hai tập hợp:  Tập hợp C gồm các phần tử thuộc A hoặc thuộc B được gọi là hợp của A và B.

Kí hiệu: \(A \cup B\)

3) Hiệu và phần bù của hai tập hợp:

Tập hợp C gồm các phần tử thuộc A nhưng không thuộc B gọi là hiệu của A và B.

Khi \(B \subset A\) thi A\B được gọi là phần bù của B trong A, kí hiệu \({C_A}B\)

Lời giải chi tiết:

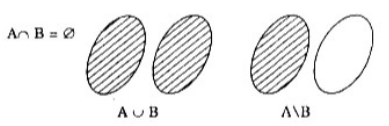
LG c

Phương pháp giải:

1) Giao của hai tập hơp: Tập hợp C gồm các phần tử vừa thuộc A, vừa thuộc B được gọi là giao của A và B.

Kí hiệu: \(A \cap B\)

2) Hợp của hai tập hợp:  Tập hợp C gồm các phần tử thuộc A hoặc thuộc B được gọi là hợp của A và B.

Kí hiệu: \(A \cup B\)

3) Hiệu và phần bù của hai tập hợp:

Tập hợp C gồm các phần tử thuộc A nhưng không thuộc B gọi là hiệu của A và B.

Khi \(B \subset A\) thi A\B được gọi là phần bù của B trong A, kí hiệu \({C_A}B\)

Lời giải chi tiết:

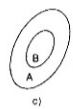
LG d

Phương pháp giải:

1) Giao của hai tập hơp: Tập hợp C gồm các phần tử vừa thuộc A, vừa thuộc B được gọi là giao của A và B.

Kí hiệu: \(A \cap B\)

2) Hợp của hai tập hợp:  Tập hợp C gồm các phần tử thuộc A hoặc thuộc B được gọi là hợp của A và B.

Kí hiệu: \(A \cup B\)

3) Hiệu và phần bù của hai tập hợp:

Tập hợp C gồm các phần tử thuộc A nhưng không thuộc B gọi là hiệu của A và B.

Khi \(B \subset A\) thi A\B được gọi là phần bù của B trong A, kí hiệu \({C_A}B\)

Lời giải chi tiết:

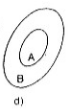
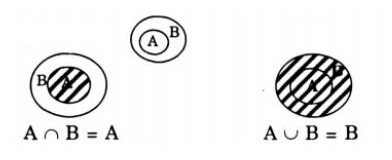
Tập \(A\) nằm trong tập \(B\) do đó \(A\subset B\) suy ra \(A\backslash B=\phi\)