Bài 2 trang 13 SGK Đại số 10

Trong hai tập hợp \(A\) và \(B\) dưới đây, tập hợp nào là con của tập hợp còn lại? Hai tập hợp \(A\) và \(B\) có bằng nhau không?

LG a

\(A\) là tập hợp các hình vuông

\(B\) là tập hợp các hình thoi.

Phương pháp giải:

Nếu mọi phần tử của tập hợp A đều là phần tử của tập hợp B thì ta nói A là một tập hợp con của B và viết là: \(A \subset B\) (đọc là A chứa trong B).

Hai tập hợp bằng nhau: Khi \(A \subset B\) và \(B \subset A\) ta nói tập hợp A bằng tập hợp B và viết là: A = B

Lời giải chi tiết:

Mỗi hình vuông là một hình thoi (có một góc vuông). Vậy \(A ⊂ B, A ≠ B\).

LG b

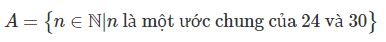
\(B = \left\{ n ∈ \mathbb N| n \text { là một ước của } 6\right\}\).

Phương pháp giải:

Nếu mọi phần tử của tập hợp A đều là phần tử của tập hợp B thì ta nói A là một tập hợp con của B và viết là: \(A \subset B\) (đọc là A chứa trong B).

Hai tập hợp bằng nhau: Khi \(A \subset B\) và \(B \subset A\) ta nói tập hợp A bằng tập hợp B và viết là: A = B

Lời giải chi tiết:

Mỗi số là ước của \(6\) là một ước chung của \(24\) và \(30\).

\(n ∈ B \Rightarrow n ∈ A\). Vậy \(B ⊂ A\).

\(24\) và \(30\) có ước chung lớn nhất là \(6\), do đó mỗi ước chung của \(24\) và \(30\) là một ước của \(6\). Vậy \(A ⊂ B\). Suy ra \(A= B\).