Bài 18 trang 52 SGK Toán 9 tập 1
Giải bài 18 trang 52 SGK Toán 9 tập 1. Biết rằng với x = 4 thì hàm số y = 3x + b có giá trị là 11...
Đề bài
a) Biết rằng với \(x = 4\) thì hàm số \(y = 3x + b\) có giá trị là \(11\). Tìm \(b\). Vẽ đồ thị của hàm số với giá trị \(b\) vừa tìm được.
b) Biết rằng đồ thị của hàm số \(y = ax + 5\) đi qua điểm \(A (-1; 3)\). Tìm a. Vẽ đồ thị của hàm số với giá trị \(a\) vừa tìm được.
Phương pháp giải - Xem chi tiết
a) Thay giá trị của \(x,\ y\) đã biết vào công thức hàm số ta tìm được \(b\).
b) Thay tọa độ điểm \(A\) vào công thức hàm số ta tìm được \(a\).
* Cách vẽ đồ thị hàm số \(y=ax+b,\ (a \ne 0)\): Đồ thị hàm số \(y=ax+b \, \, (a\neq 0)\) là đường thẳng:
+) Cắt trục hoành tại điểm \(A(-\dfrac{b}{a}; \, 0).\)
+) Cắt trục tung tại điểm \(B(0;b).\)
Xác định tọa độ hai điểm \(A\) và \(B\) sau đó kẻ đường thẳng đi qua hai điểm đó ta được đồ thị hàm số \(y=ax+b \, \, (a\neq 0).\)
Lời giải chi tiết
a) Thay \(x = 4\) và \(y = 11\) vào \(y = 3x +b\), ta được:
\(11 = 3.4 + b\)
\(\Leftrightarrow 11=12+b\)
\(\Leftrightarrow 11- 12 =b\)
\(\Leftrightarrow b=-1\).
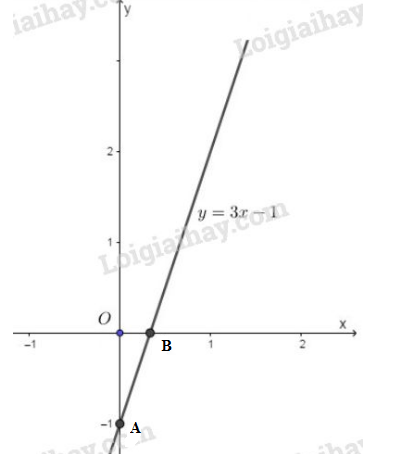
Khi đó hàm số đã cho trở thành: \(y = 3x – 1\).
+ Cho \(x=0 \Rightarrow y=3.0 - 1=-1 \Rightarrow A(0; -1)\)
Cho \( y=0 \Rightarrow 0=3.x - 1 \Rightarrow x=\dfrac{1}{3} \Rightarrow B{\left(\dfrac{1}{3}; 0 \right)}\)
Do đó đồ thị hàm số \(y=3x+b\) là đường thẳng đi qua \(2\) điểm \(A(0;-1)\) và \(B\left( {\dfrac{1}{3};0} \right)\). Ta có hình vẽ sau:
b) Thay \(x= -1 \) thì \(y=3\) thay vào công thức hàm số \(y=ax+5\), ta được:
\( 3= a.(-1) + 5 \)
\(\Leftrightarrow 3 = -a +5\)
\(\Leftrightarrow a = 5-3\)
\(\Leftrightarrow a = 2\)
Khi đó hàm số đã cho trở thành: \(y = 2x + 5\).
+ Cho \(x = 0 \Rightarrow y = 2.0 +5=5 \Rightarrow A(0; 5)\)
Cho \(y=0 \Rightarrow 0= 2. x +5 \Rightarrow x=\dfrac{-5}{2} \Rightarrow B {\left(-\dfrac{5}{2}; 0 \right)}\)
Do đó đồ thị hàm số là đường thẳng đi qua hai điểm \(A(0; 5)\) và \(B \left( { - \dfrac{5}{2};0} \right)\).

Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 18 trang 52 SGK Toán 9 tập 1 timdapan.com"