Bài 11 trang 60 SGK Hình học 10

Đề bài

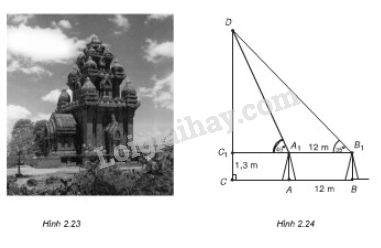
Muốn đo chiều cao của tháp Chàm Por Klong Garai ở Ninh Thuận, người ta lấy hai điểm \(A\) và \(B\) trên mặt đất có khoảng cách \(AB = 12m\) cùng thẳng hàng với chân \(C\) của tháp để đặt hai giác kế. Chân của giác kế có chiều cao \(h = 1,3m\). Gọi \(D\) là đỉnh tháp và hai điểm \(A_1, \, B_1\) cùng thẳng  hàng với \(C_1\) thuộc chiều cao \(CD\) của tháp. Người ta đo được \(\widehat {D{A_1}{C_1}} = {49^0}\) và \(\widehat {D{B_1}{C_1}} = {35^0}.\) Tính chiều cao của  \(CD\) của tháp đó.

Lời giải chi tiết

Ta có: \(A_1B_1=Ab=12m.\)

Xét \(\Delta DC_1A_1\) có: \(C_1A_1=C_1D.\cot 49^0\)

Xét \(\Delta DC_1B_1\) có: \(C_1B_1=C_1D.\cot 35^0\)

Mà \(A_1B_1=C_1B_1-C_1A_1\)\(=C_1D.\cot 35^0-C_1D.\cot 49^0\)

      \(=C_1D(\cot 35^0 - \cot 49^0).\)

\(\Rightarrow C_1D=\frac{A_1B_1}{\cot 35^0 - \cot 49^0}  =\frac{12}{\cot 35^0 - \cot 49^0}\)\(\approx 21,47 \, m. \)

Vậy chiều cao \(CD\) của tháp là: 

\(DC = 1,3 + 21,47= 22,77m.\)