Lý thuyết Vecto trong không gian Toán 12 Kết nối tri thức

1. Vecto trong không gian

1. Vecto trong không gian

Khái niệm vecto trong không gian

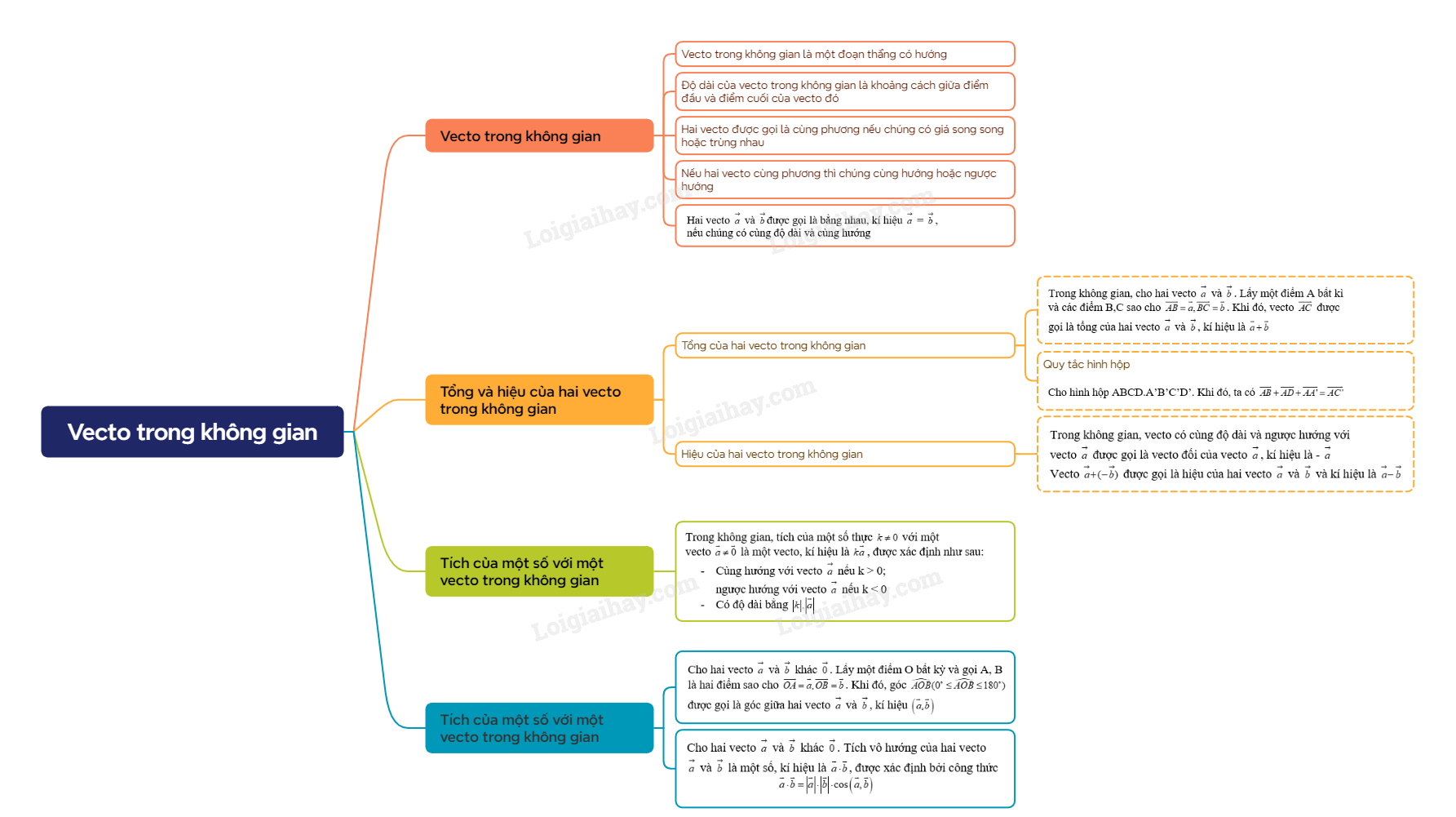
- Vecto trong không gian là một đoạn thẳng có hướng

- Độ dài của vecto trong không gian là khoảng cách giữa điểm đầu và điểm cuối của vecto đó

- Hai vecto được gọi là cùng phương nếu chúng có giá song song hoặc trùng nhau

- Nếu hai vecto cùng phương thì chúng cùng hướng hoặc ngược hướng

- Hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \)được gọi là bằng nhau, kí hiệu \(\mathop a\limits^ \to \) = \(\mathop b\limits^ \to \), nếu chúng có cùng độ dài và cùng hướng

2. Tổng và hiệu của hai vecto trong không gian

a) Tổng của hai vecto trong không gian

Trong không gian, cho hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \). Lấy một điểm A bất kì và các điểm B,C sao cho \(\overrightarrow {AB} = \overrightarrow a ,\overrightarrow {BC} = \overrightarrow b \). Khi đó, vecto \(\overrightarrow {AC} \) được gọi là tổng của hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \), kí hiệu là \(\overrightarrow a + \overrightarrow b \)

Trong không gian, phép lấy tổng của hai vecto được gọi là phép cộng vecto

Quy tắc hình hộp

Cho hình hộp ABCD.A’B’C’D’. Khi đó, ta có \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC'} \)

b) Hiệu của hai vecto trong không gian

Trong không gian, vecto có cùng độ dài và ngược hướng với vecto \(\mathop a\limits^ \to \) được gọi là vecto đối của vecto \(\mathop a\limits^ \to \), kí hiệu là - \(\mathop a\limits^ \to \)

Vecto \(\mathop a\limits^ \to + ( - \mathop b\limits^ \to )\) được gọi là hiệu của hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \) và kí hiệu là \(\mathop a\limits^ \to - \mathop b\limits^ \to \)

Trong không gian, phép lấy hiệu của hai vecto được gọi là phép trừ vecto

3. Tích của một số với một vecto trong không gian

Trong không gian, tích của một số thực \(k \ne 0\) với một vecto \(\overrightarrow a \ne \overrightarrow 0 \) là một vecto, kí hiệu là \(k\overrightarrow a \), được xác định như sau:

- Cùng hướng với vecto \(\mathop a\limits^ \to \) nếu k > 0; ngược hướng với vecto \(\mathop a\limits^ \to \) nếu k < 0

- Có độ dài bằng \(\left| k \right|.\left| {\overrightarrow a } \right|\)

Trong không gian, phép lấy tích của một số với một vecto được gọi là phép nhân một số với một vecto

4. Tích của một số với một vecto trong không gian

a) Góc giữa hai vecto trong không gian

Trong không gian, cho hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \) khác \(\mathop 0\limits^ \to \). Lấy một điểm O bất kỳ và gọi A, B là hai điểm sao cho \(\overrightarrow {OA} = \overrightarrow a ,\overrightarrow {OB} = \overrightarrow b \). Khi đó, góc \(\widehat {AOB}({0^ \circ } \le \widehat {AOB} \le {180^ \circ })\) được gọi là góc giữa hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \), kí hiệu \(\left( {\overrightarrow a ,\overrightarrow b } \right)\)

b) Tích vô hướng của hai vecto trong không gian

Trong không gian, cho hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \) khác \(\mathop 0\limits^ \to \). Tích vô hướng của hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \) là một số, kí hiệu là \(\overrightarrow a \cdot \overrightarrow b \), được xác định bởi công thức

\(\overrightarrow a \cdot \overrightarrow b = \left| {\overrightarrow a } \right| \cdot \left| {\overrightarrow b } \right| \cdot \cos \left( {\overrightarrow a ,\overrightarrow b } \right)\)