Giải bài tập 2.2 trang 58 SGK Toán 12 tập 1 - Kết nối tri thức

Đề bài

Cho hình hộp chữ nhật ABCD.A’B’C’D’ có \(AB = 2,AD = 3\) và \(AA' = 4\). Tính độ dài của các vectơ \(\overrightarrow {BB'} ,\overrightarrow {BD} \) và \(\overrightarrow {BD'} \).

Lời giải chi tiết

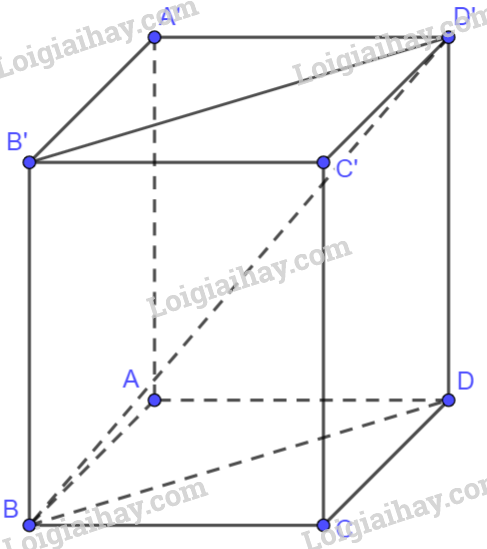
Vì B’BAA’ là hình chữ nhật nên \(BB' = AA' = DD' = 4 \Rightarrow \left| {\overrightarrow {BB'} } \right| = 4\)

Vì tứ giác ABCD là hình chữ nhật nên tam giác BAD vuông tại A.

Do đó, \(BD = \sqrt {A{B^2} + A{D^2}}  = \sqrt {{2^2} + {3^2}}  = \sqrt {13} \) (định lí Pythagore), suy ra: \(\left| {\overrightarrow {BD} } \right| = \sqrt {13} \)

Vì BB’D’D là hình chữ nhật nên tam giác DD’B vuông tại D

Theo định lí Pythagore ta có: \(BD' = \sqrt {B{D^2} + DD{'^2}}  = \sqrt {13 + {4^2}}  = \sqrt {29}  \Rightarrow \left| {\overrightarrow {BD'} } \right| = \sqrt {29} \)