Lý thuyết Góc giữa đường thẳng và mặt phẳng, góc nhị diện - Toán 11 Cánh diều

1. Góc giữa đường thẳng và mặt phẳng

Cho đường thẳng d và mặt phẳng (P), ta có định nghĩa sau:

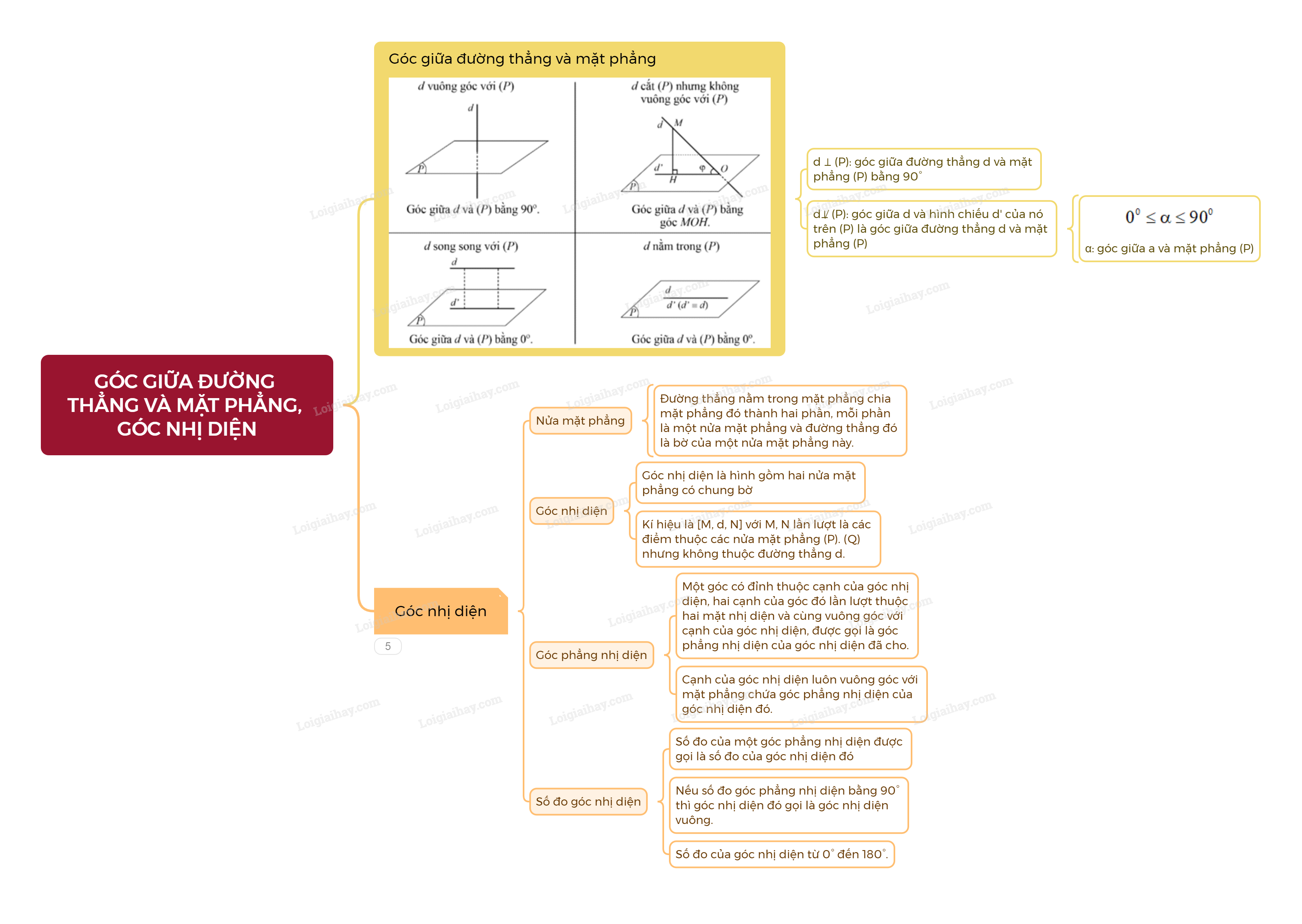
- Nếu đường thẳng d vuông góc với mặt phẳng (P) thì góc giữa d và (P) bằng \({90^0}\).

- Nếu đường thẳng d không vuông góc với mặt phẳng (P) thì góc giữa đường thẳng d và mặt phẳng (P) là góc giữa d và hình chiếu d’ của đường thẳng d trên (P).

Nhận xét: Góc giữa đường thẳng và mặt phẳng có số đo từ \({0^0}\) đến \({90^0}\).

2. Góc nhị diện

a) Nửa mặt phẳng

Một đường thẳng nằm trong mặt phẳng chia mặt phẳng đó thành hai phần, mỗi phần được gọi là một nửa mặt phẳng và đường thẳng đó được gọi là bờ của một nửa mặt phẳng này.

b) Góc nhị diện

Góc nhị diện là hình gồm hai nửa mặt phẳng có chung bờ.

Ví dụ:  Xét góc nhị diện gồm hai nửa mặt phẳng (P) và (Q) có chung bờ là đường thẳng d, kí hiệu là [P, d, Q]. Đường thẳng d gọi là cạnh của góc nhị diện, mỗi nửa mặt phẳng (P) và (Q) gọi là một mặt của góc nhị diện.

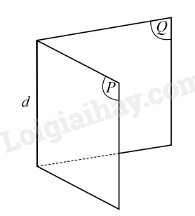
Chú ý: Góc nhị diện còn được kí hiệu là [M, d, N] với M, N lần lượt là các điểm thuộc các nửa mặt phẳng (P). (Q) nhưng không thuộc đường thẳng d.

c) Góc phẳng nhị diện

Trong không gian, cho góc nhị diện. Một góc có đỉnh thuộc cạnh của góc nhị diện, hai cạnh của góc đó lần lượt thuộc hai mặt nhị diện và cùng vuông góc với cạnh của góc nhị diện, được gọi là góc phẳng nhị diện của góc nhị diện đã cho.

Ví dụ: Cho góc nhị diện [P, d, Q]. Lấy O thuộc d, hai tia Ox, Oy lần lượt nằm trên hai nửa mặt phẳng (P), (Q) và cùng vuông góc với d. Khi đó góc xOy là góc phẳng nhị diện của góc nhị diện [P, d, Q].

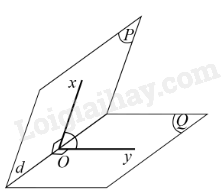
Nhận xét: Cạnh của góc nhị diện luôn vuông góc với mặt phẳng chứa góc phẳng nhị diện của góc nhị diện đó.

d) Số đo của góc nhị diện

- Số đo của một góc phẳng nhị diện được gọi là số đo của góc nhị diện đó.

- Nếu số đo góc phẳng nhị diện bằng 90° thì góc nhị diện đó gọi là góc nhị diện vuông.

Nhận xét: Số đo của góc nhị diện từ \({0^0}\) đến \({180^0}\).