Lý thuyết Đường thẳng và mặt phẳng song song - SGK Toán 11 Cùng khám phá

1. Đường thẳng và mặt phẳng song song trong không gian

 * Đường thẳng và mặt phẳng được gọi là song song nếu chúng không có điểm chung.

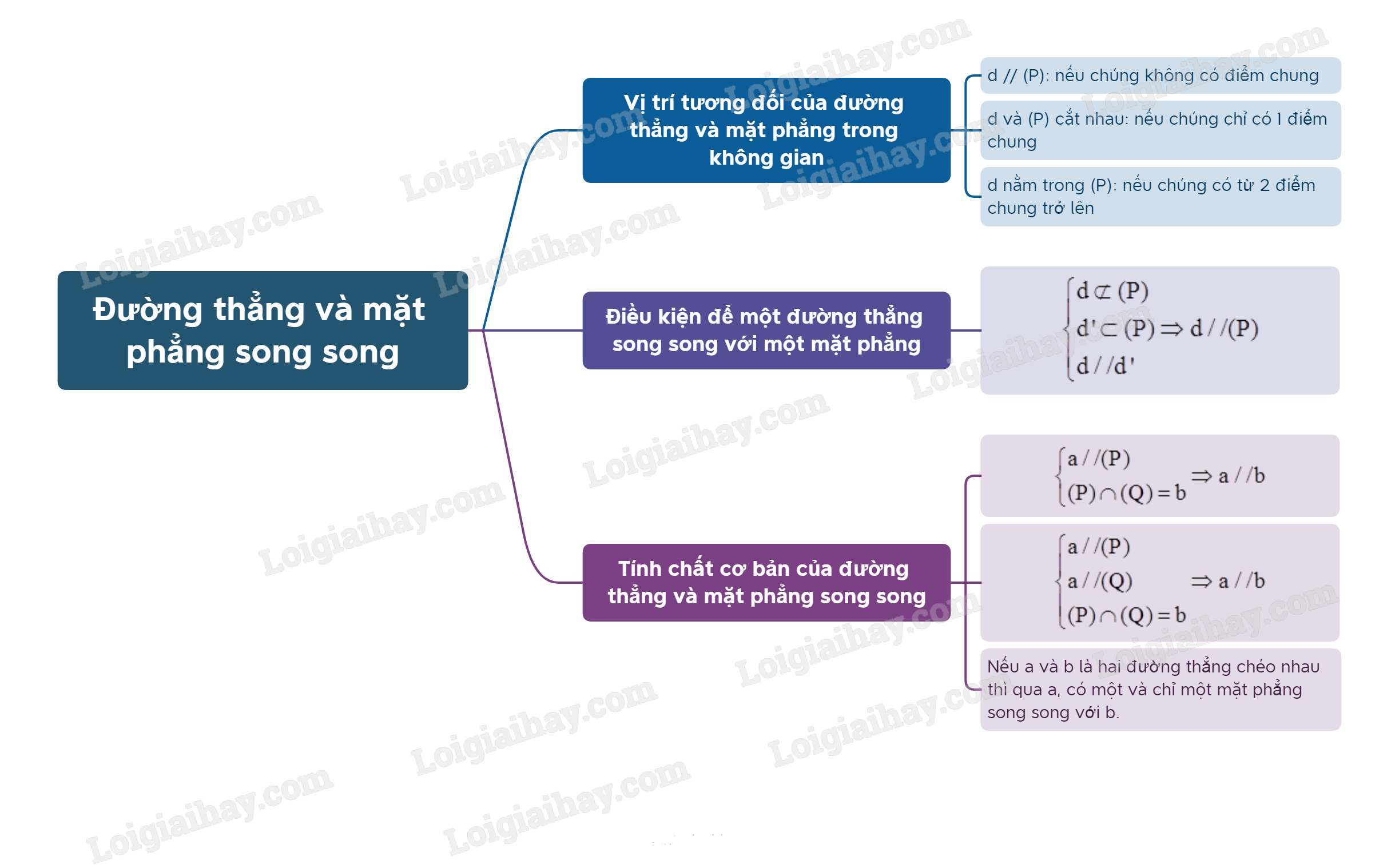
- Cho đường thẳng d và \(\left( \alpha  \right)\). Tùy vào số điểm chung của  đường thẳng d và \(\left( \alpha  \right)\), ta có các vị trí tương đối sau:

II. Điều kiện để một đường thẳng và mặt phẳng song song

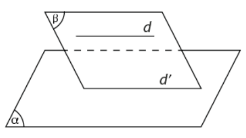
• Điều kiện để đường thẳng song song với mặt phẳng: Nếu đường thẳng d không nằm trong mặt phẳng \(\left( \alpha  \right)\) và song song với một đường thẳng d’ nào đó nằm trong \(\left( \alpha  \right)\) thì ta nói \(d//\left( \alpha  \right)\).

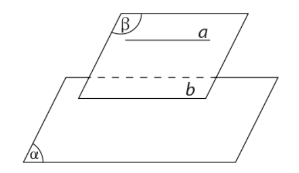
• Cho đường thẳng a song song với mặt phẳng \(\left( \alpha  \right)\). Nếu mặt phẳng \(\left( \beta  \right)\)chứa a và cắt \(\left( \alpha  \right)\)theo giao tuyến b thì a // b.

* Hệ quả:

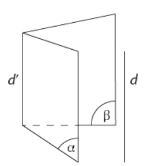
- Nếu hai mặt phẳng phân biệt cùng song song với một đường thẳng thì giao tuyến của chúng (nếu có) cũng song song với đường thẳng đó.

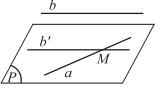
• Nếu a và b là hai đường thẳng chéo nhau thì qua a, có một và chỉ một mặt phẳng song song với b.