Giải mục 1 trang 74, 75, 76 SGK Toán 9 tập 1 - Cánh diều

HĐ1

Trả lời câu hỏi Hoạt động 1 trang 74 SGK Toán 9 Cánh diều

Cho tam giác \(ABC\) vuông tại \(A\) có \(\widehat B = \alpha \) (Hình 2).

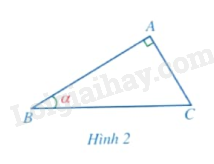
a) Cạnh góc vuông nào là cạnh đối của góc \(B\)?

b) Cạnh góc vuông nào là cạnh kề của góc \(B\)?

c) Cạnh nào là cạnh huyền?

Phương pháp giải:

Dựa vào kiến thức đã học về tam giác vuông để trả lời câu hỏi.

Lời giải chi tiết:

a) Cạnh góc vuông là cạnh đối của góc \(B\) là \(AC\).

b) Cạnh góc vuông là cạnh kể của góc \(B\) là \(AB\).

c) Cạnh huyền là cạnh \(BC\).

LT1

Trả lời câu hỏi Luyện tập 1 trang 77 SGK Toán 9 Cánh diều

Cho tam giác \(MNP\) vuông tại \(M,MN = 3cm,MP = 4cm\). Tính độ dài cạnh \(NP\) và các tỉ số lượng giác của góc \(P\).

Phương pháp giải:

+ Dựa vào định lí Pythagore để tính cạnh \(NP\).

+ Dựa vào kiến thức đã học về tỉ số lượng giác để tính các tỉ số lượng giác của góc \(P\).

Lời giải chi tiết:

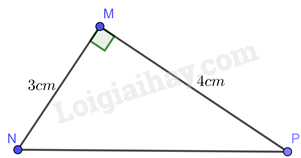
Xét tam giác \(MNP\) vuông tại \(M\), ta có:

\(NP = \sqrt {{3^2} + {4^2}}  = \sqrt {25}  = 5\left( {cm} \right)\)

Tam giác \(MNP\) vuông tại \(M\) nên:

+ \(\cos \widehat P = \frac{{MP}}{{NP}} = \frac{4}{5}\).

+ \(\sin \widehat P = \frac{{MN}}{{NP}} = \frac{3}{5}.\)

+ \(\tan \widehat P = \frac{{MN}}{{MP}} = \frac{3}{4}.\)

+ \(\cot \widehat P = \frac{{MP}}{{MN}} = \frac{4}{3}.\)