Bài tập trắc nghiệm trang 203, 204, 205 SBT đại số và giải tích 11

Chọn đáp án đúng:

5.30

Tính y', biết y = x⁵ - 4x³ - x² + x/2

A. y' = 5x⁴ - 12x² - 2x + 1/2

B. y' = 5x⁴ - 10x² + 1/2

C. y' = 5x⁴ - 2x

D. y' = 5x⁴ + 12x⁴ - 2x - 1/2

Lời giải chi tiết:

\(\begin{array}{l}y' = 5{x^4} - 4.3{x^2} - 2x + \dfrac{1}{2}\\ = 5{x^4} - 12{x^2} - 2x + \dfrac{1}{2}\end{array}\)

Chọn đáp án: A

5.31

\(y =  - 6\sqrt x  + \dfrac{3}{x}\). Tìm y'.

A. \(y' = \dfrac{3}{{\sqrt x }}\)

B. \(y' =  - \dfrac{3}{{\sqrt x }} - \dfrac{3}{{{x^2}}}\)

C. \(y' = \dfrac{3}{{\sqrt x }} - 5\)

D. \(y' =  - \dfrac{3}{{\sqrt x }} + \dfrac{3}{x}\)

Lời giải chi tiết:

\(\begin{array}{l}y' =  - 6.\dfrac{1}{{2\sqrt x }} - \dfrac{3}{{{x^2}}}\\ =  - \dfrac{3}{{\sqrt x }} - \dfrac{3}{{{x^2}}}\end{array}\)

Chọn đáp án: B

5.32

Tính đạo hàm của hàm số \(y = \dfrac{{2x - 3}}{{x + 4}}\)

A. \(y' = \dfrac{{10}}{{{{\left( {x + 4} \right)}^2}}}\)

B. \(y' = \dfrac{{11}}{{{{\left( {x + 4} \right)}^2}}}\)

C. \(y' = \dfrac{5}{{{{\left( {x + 4} \right)}^2}}}\)

D. \(y' = \dfrac{{ - 11}}{{{{\left( {x + 4} \right)}^2}}}\)

Lời giải chi tiết:

\(\begin{array}{l}y' = \dfrac{{\left( {2x - 3} \right)'\left( {x + 4} \right) - \left( {2x - 3} \right)\left( {x + 4} \right)'}}{{{{\left( {x + 4} \right)}^2}}}\\ = \dfrac{{2\left( {x + 4} \right) - \left( {2x - 3} \right)}}{{{{\left( {x + 4} \right)}^2}}}\\ = \dfrac{{11}}{{{{\left( {x + 4} \right)}^2}}}\end{array}\)

Chọn đáp án: B

5.33

Cho hàm số \(y = x\sqrt {1 + {x^2}} \) . Tính y'.

A. \(y' = \dfrac{{1 - 2{x^2}}}{{\sqrt {1 + {x^2}} }}\)

B. \(y' = \dfrac{{1 + 2{x^2}}}{{\sqrt {1 - {x^2}} }}\)

C. \(y' = \dfrac{{1 + 2{x^2}}}{{1 + {x^2}}}\)

D. \(y' = \dfrac{{1 + 2{x^2}}}{{\sqrt {1 + {x^2}} }}\)

Lời giải chi tiết:

\(\begin{array}{l}y' = \left( x \right)'.\sqrt {1 + {x^2}}  + x.\left( {\sqrt {1 + {x^2}} } \right)'\\ = \sqrt {1 + {x^2}}  + x.\dfrac{{\left( {1 + {x^2}} \right)'}}{{2\sqrt {1 + {x^2}} }}\\ = \sqrt {1 + {x^2}}  + x.\dfrac{{2x}}{{2\sqrt {1 + {x^2}} }}\\ = \sqrt {1 + {x^2}}  + \dfrac{{{x^2}}}{{\sqrt {1 + {x^2}} }}\\ = \dfrac{{1 + {x^2} + {x^2}}}{{\sqrt {1 + {x^2}} }} = \dfrac{{1 + 2{x^2}}}{{\sqrt {1 + {x^2}} }}\end{array}\)

Chọn đáp án: D

5.34

Cho f(x) = 5 - 3x - x². Tính f'(0), f'(-2).

A. -3; 0            B. -2; 1

C. -3; 1            D. 3; 2

Lời giải chi tiết:

\(\begin{array}{l}f'\left( x \right) =  - 3 - 2x\\f'\left( 0 \right) =  - 3 - 2.0 =  - 3\\f'\left( { - 2} \right) =  - 3 - 2.\left( { - 2} \right) = 1\end{array}\)

Chọn đáp án: C

5.35

Cho hàm số \(y = \sqrt {{x^3} - 2{x^2} + 1} \) . Tìm y'.

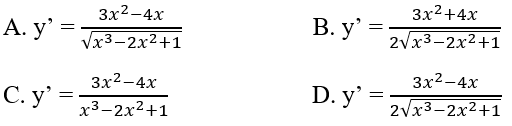
Lời giải chi tiết:

\(\begin{array}{l}y' = \dfrac{{\left( {{x^3} - 2{x^2} + 1} \right)'}}{{2\sqrt {{x^3} - 2{x^2} + 1} }}\\ = \dfrac{{3{x^2} - 2.2x}}{{2\sqrt {{x^3} - 2{x^2} + 1} }}\\ = \dfrac{{3{x^2} - 4x}}{{2\sqrt {{x^3} - 2{x^2} + 1} }}\end{array}\)

Chọn đáp án: D

5.36

Cho f(x) = x⁵ + x³ - 2x + 3. Tính f'(1), f'(0).

A. 6; 2            B. 6; -2

C. 6; 6            D. -2; 6

Lời giải chi tiết:

\(\begin{array}{l}f'\left( x \right) = 5{x^4} + 3{x^2} - 2\\f'\left( 1 \right) = 5 + 3 - 2 = 6\\f'\left( 0 \right) = 5.0 + 3.0 - 2 =  - 2\end{array}\)

Chọn đáp án: B

5.37

Giải bất phương trình φ'(x) < 0 với \(\varphi \left( x \right) = \dfrac{{2x - 1}}{{{x^2} + 1}}\)

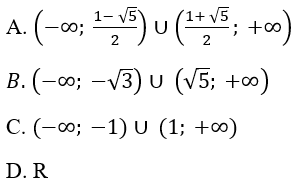
Lời giải chi tiết:

\(\begin{array}{l}\varphi '\left( x \right)\\ = \dfrac{{\left( {2x - 1} \right)'\left( {{x^2} + 1} \right) - \left( {2x - 1} \right)\left( {{x^2} + 1} \right)'}}{{{{\left( {{x^2} + 1} \right)}^2}}}\\ = \dfrac{{2\left( {{x^2} + 1} \right) - \left( {2x - 1} \right).2x}}{{{{\left( {{x^2} + 1} \right)}^2}}}\\ = \dfrac{{2{x^2} + 2 - 4{x^2} + 2x}}{{{{\left( {{x^2} + 1} \right)}^2}}}\\ = \dfrac{{ - 2{x^2} + 2x + 2}}{{{{\left( {{x^2} + 1} \right)}^2}}}\\\varphi '\left( x \right) < 0\\ \Leftrightarrow \dfrac{{ - 2{x^2} + 2x + 2}}{{{{\left( {{x^2} + 1} \right)}^2}}} < 0\\ \Leftrightarrow  - 2{x^2} + 2x + 2 < 0\\ \Leftrightarrow \left[ \begin{array}{l}x > \dfrac{{1 + \sqrt 5 }}{2}\\x < \dfrac{{1 - \sqrt 5 }}{2}\end{array} \right.\end{array}\)

Chọn đáp án: A

5.38

Tính \(f'\left( 1 \right)\) biết \(f\left( x \right) = \dfrac{1}{x} + \dfrac{2}{{{x^2}}} + \dfrac{3}{{{x^3}}}\)

A. 6                 B. 10

C. 9                 D. -14

Lời giải chi tiết:

\(\begin{array}{l}f'\left( x \right) =  - \dfrac{1}{{{x^2}}} + \dfrac{{ - 2\left( {{x^2}} \right)'}}{{{x^4}}} + \dfrac{{ - 3\left( {{x^3}} \right)'}}{{{x^6}}}\\ =  - \dfrac{1}{{{x^2}}} - \dfrac{{2.2x}}{{{x^4}}} - \dfrac{{3.3{x^2}}}{{{x^6}}}\\ =  - \dfrac{1}{{{x^2}}} - \dfrac{4}{{{x^3}}} - \dfrac{9}{{{x^4}}}\\ \Rightarrow f'\left( 1 \right) =  - 1 - 4 - 9 =  - 14\end{array}\)

Chọn đáp án: D

5.39

Tính h'(0), biết rằng \(h\left( x \right) = \dfrac{x}{{\sqrt {4 - {x^2}} }}\)

A. 2            B. -1            C. 1/2            D. 4

Lời giải chi tiết:

\(\begin{array}{l}h'\left( x \right)\\ = \dfrac{{\left( x \right)'.\sqrt {4 - {x^2}}  - x.\left( {\sqrt {4 - {x^2}} } \right)'}}{{{{\left( {\sqrt {4 - {x^2}} } \right)}^2}}}\\ = \dfrac{{\sqrt {4 - {x^2}}  - x.\dfrac{{\left( {4 - {x^2}} \right)'}}{{2\sqrt {4 - {x^2}} }}}}{{4 - {x^2}}}\\ = \dfrac{{\sqrt {4 - {x^2}}  - x.\dfrac{{ - 2x}}{{2\sqrt {4 - {x^2}} }}}}{{4 - {x^2}}}\\ = \dfrac{{\sqrt {4 - {x^2}}  + \dfrac{{{x^2}}}{{\sqrt {4 - {x^2}} }}}}{{4 - {x^2}}}\\ = \dfrac{{4 - {x^2} + {x^2}}}{{\left( {4 - {x^2}} \right)\sqrt {4 - {x^2}} }}\\ = \dfrac{4}{{\left( {4 - {x^2}} \right)\sqrt {4 - {x^2}} }}\\ \Rightarrow h'\left( 0 \right) = \dfrac{4}{{\left( {4 - 0} \right)\sqrt {4 - 0} }} = \dfrac{1}{2}\end{array}\)

Chọn đáp án: C