Bài 92 trang 150 SBT toán 7 tập 1
Giải bài 92 trang 150 sách bài tập toán 7 tập 1. Chứng minh rằng tam giác ABC vẽ trên giấy kẻ ô vuông (hình 67) là tam giác vuông cân.
Đề bài
Chứng minh rằng tam giác \(ABC\) vẽ trên giấy kẻ ô vuông (hình 67) là tam giác vuông cân.
Phương pháp giải - Xem chi tiết
- Áp dụng định lí Pytago: Bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.
- Định lí Pytago đảo: Nếu một tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông.
Lời giải chi tiết
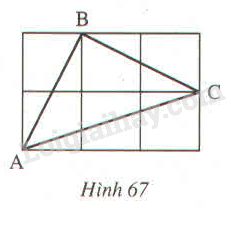
Đặt độ dài cạnh mỗi ô vuông là \(1\) (đơn vị độ dài)
Áp dụng định lí Pytago ta có:
\(\eqalign{
& {\rm{A}}{B^2} = {1^2} + {2^2} = 1 + 4 = 5 \cr
& B{C^2} = {1^2} + {2^2} = 1 + 4 = 5 \cr
& A{C^2} = {3^2} + {1^2} = 9 + 1 = 10 \cr} \)
\( \Rightarrow A{C^2} = A{B^2} + B{C^2}\)
Theo định lí Pytago đảo ta có \(∆ABC\) vuông tại \(B.\)
Mặt khác: \(A{B^2} = B{C^2} = 5\)
\( \Rightarrow AB = BC\) (vì độ dài đoạn thẳng luôn dương).
Vậy \(∆ABC\) vuông cân tại \(B.\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 92 trang 150 SBT toán 7 tập 1 timdapan.com"







