Bài 83 trang 149 SBT toán 7 tập 1
Giải bài 83 trang 149 sách bài tập toán 7 tập 1. Cho tam giác nhọn ABC. Kẻ AH vuông góc với BC. Tính chu vi tam giác ABC biết AC = 20cm, AH = 12cm, BH = 5cm.
Đề bài
Cho tam giác nhọn \(ABC.\) Kẻ \(AH\) vuông góc với \(BC.\) Tính chu vi tam giác \(ABC\) biết \(AC = 20cm, AH = 12cm, \) \(BH = 5cm\).
Phương pháp giải - Xem chi tiết
- Áp dụng định lí Pytago: Bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.
- Chu vi tam giác bằng tổng độ dài ba cạnh của tam giác đó.
Lời giải chi tiết
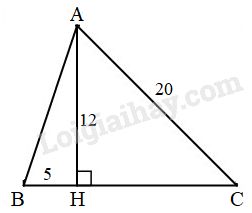
Áp dụng định lý Pytago vào \(∆AHB\) có \(\widehat {AHB} = 90^\circ \), ta có:
\( A{B^2} = A{H^2} + H{B^2} \)
\( \Rightarrow A{B^2} = {12^2} + {5^2} = 169 \)
\(\Rightarrow AB = 13 (cm)\)
Áp dụng định lý Pytago vào \(∆AHC\) có \(\widehat {AHC} = 90^\circ \), ta có:
\(A{C^2} = A{H^2} + H{C^2} \)
\( \Rightarrow H{C^2} = A{C^2} - A{H^2} \)
\( \Rightarrow H{C^2}= {20^2} - {12^2} = 256 \)
\( \Rightarrow HC = 16(cm)\).
Ta có: \(BC = BH + HC = 5 + 16 = 21\, (cm)\)
Chu vi tam giác \(ABC\) là:
\(AB + AC + BC = 13 + 20 + 21 = 54\)\(\, (cm)\).
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 83 trang 149 SBT toán 7 tập 1 timdapan.com"







