Bài 9.2 phần bài tập bổ sung trang 95 SBT toán 8 tập 1
Giải bài 9.2 phần bài tập bổ sung trang 95 sách bài tập toán 8. Cho tam giác ABC vuông tại A, đường cao AH. Gọi I, K theo thứ tự là trung điểm của AB, AC. Tính số đo góc IHK.
Đề bài
Cho tam giác \(ABC\) vuông tại \(A,\) đường cao \(AH.\) Gọi \(I,\, K\) theo thứ tự là trung điểm của \(AB,\, AC.\) Tính số đo góc \(IHK.\)
Phương pháp giải - Xem chi tiết
Tính chất đường trung tuyến ứng với cạnh huyền trong tam giác vuông: Trong tam giác vuông đường trung tuyến tuyến ứng với cạnh huyền bằng nửa cạnh ấy.
Lời giải chi tiết
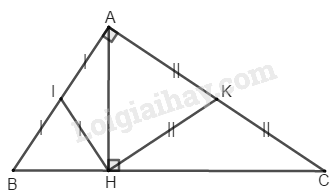
\(∆ AHB\) vuông tại \(H\) có \(HI\) là đường trung tuyến thuộc cạnh huyền \(AB\)
\(⇒ HI = IA = \dfrac{1}{2}AB\) (tính chất tam giác vuông)
\(⇒ ∆ IAH\) cân tại \(I\)
\( \Rightarrow \widehat {IAH} = \widehat {IHA}\) (1)
\(∆ AHC\) vuông tại \(H\) có \(HK\) là đường trung tuyến thuộc cạnh huyền \(AC\)
\(⇒ HK = KA = \dfrac{1}{2}AC\) (tính chất tam giác vuông)
\(⇒ ∆ KAH\) cân tại \(K\) \( \Rightarrow \widehat {KAH} = \widehat {KHA}\) (2)
\(\widehat {IHK} = \widehat {IHA} + \widehat {KHA}\) (3)
Từ (1), (2) và (3) suy ra: \(\widehat {IHK} = \widehat {IAH} + \widehat {KAH}\) \(= \widehat {IAK} = \widehat {BAC} = {90^0}\).
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 9.2 phần bài tập bổ sung trang 95 SBT toán 8 tập 1 timdapan.com"







