Bài 117 trang 94 SBT toán 8 tập 1
Giải bài 117 trang 94 sách bài tập toán 8. Chứng minh rằng ba điểm C, B, D trên hình 18 thẳng hàng.
Đề bài
Chứng minh rằng ba điểm \(C,\, B,\, D\) trên hình 18 thẳng hàng.
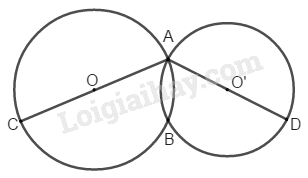
Phương pháp giải - Xem chi tiết
Tính chất đường trung tuyến ứng với cạnh huyền trong tam giác vuông:
Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.
Lời giải chi tiết
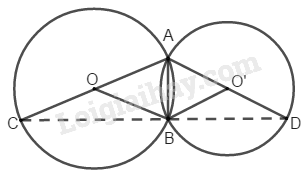
Nối \(AB,\, BO,\, BC,\, BO’,\, BD.\)
Trong \(∆ ABC\) ta có:
\(OA = OC = R\) (bán kính đường tròn \((O)\))
nên \(BO\) là đường trung tuyến của \(∆ ABC\)
mà \(BO = R\) (bán kính \((O)\))
\(⇒ BO = OA = OC = \dfrac{1}{2}AC\)
nên tam giác \(ABC\) vuông tại \(B\) \( \Rightarrow \widehat {ABC} = {90^0}\)
Trong \(∆ ABD\) ta có: \(AO’ = O’D = R’\) (bán kính \((O’)\))
nên \(BO’\) là đường trung tuyến của \(∆ ABD\)
mà \(BO’ = R’\) (bán kính \((O’)\)) \(⇒ BO’ = AO’ = O’D = \dfrac{1}{2}AD\)
nên tam giác \(ABD\) vuông tại \(B\) \( \Rightarrow \widehat {ABD} = {90^0}\)
\(\widehat {ABC} + \widehat {ABD} = \widehat {CBD}\)
\( \Rightarrow \widehat {CBD} = {90^0} + {90^0} = {180^0}\)
Vậy \(C,\, B,\, D\) thẳng hàng.
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 117 trang 94 SBT toán 8 tập 1 timdapan.com"







