Bài 89 trang 157 SBT toán 8 tập 2
Giải bài 89 trang 157 sách bài tập toán 8. Cần phải đo đường chéo của một viên gạch có dạng hình hộp chữ nhật mà chỉ được phép sử dụng thước có chia vạch thì phải làm như thế nào?
Đề bài
Cần phải đo đường chéo của một viên gạch có dạng hình hộp chữ nhật mà chỉ được phép sử dụng thước có chia vạch thì phải làm như thế nào ? (không được cắt, xẻ…)
Phương pháp giải - Xem chi tiết
Sử dụng: Một tam giác có đường cao ứng với một cạnh đồng thời là trung tuyến ứng với cạnh đó thì tam giác đó là tam giác cân.
Lời giải chi tiết
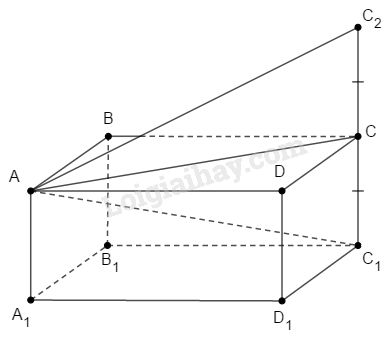
Gọi viên gạch là hình hộp chữ nhật \(ABCD.{A_1}{B_1}{C_1}{D_1}\).
Để đo đường chéo \(AC_1\) ta làm như sau:
Trên tia đối của tia \(CC_1\) ta lấy điểm \(C_2\) sao cho \(CC_2= CC_1\).
Dùng thước chia vạch đo đoạn \(AC_2\). Độ dài đoạn \(AC_2\) chính là độ dài đường chéo \(AC_1\).
Chứng minh:
Vì \(ABCD.{A_1}{B_1}{C_1}{D_1}\) là hình hộp chữ nhật nên \(CC_1\;\bot\;mp(ABCD)\) do đó \(CC_1\;\bot \;AC\)
Xét \(\Delta AC_1C_2\) có \(AC\) vừa là đường cao vừa là trung tuyến ứng với cạnh \(C_1C_2\) do đó \(\Delta AC_1C_2\) cân tại \(A\).
Suy ra \(AC_1=AC_2\) (tính chất tam giác cân).
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 89 trang 157 SBT toán 8 tập 2 timdapan.com"







