Bài 82 trang 156 SBT toán 8 tập 2

Đề bài

Cho biết hộp có dạng hình hộp chữ nhật, độ dài đường chéo là \(50cm.\) Hãy tìm các kích thước của hai hình hộp như vậy.

(HD: Đây là một bài toán mở, hãy chọn hai trong ba kích thước của hình hộp có thể chấp nhận được, từ đó tính kích thước còn lại).

Lời giải chi tiết

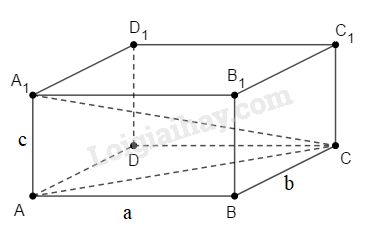
Gọi \(a, b, c\) lần lượt là ba kích thước của hình hộp chữ nhật.

Áp dụng định lí Pytago vào tam giác vuông \(ABC\), ta có:

\(A{C^2} = A{B^2} + B{C^2} = {a^2} + {b^2}\)

Áp dụng định lí Pytago vào tam giác vuông \(AA_1C\), ta có:

\({A_1}{C^2} = A{C^2} + AA_1^2 \)\(\,= {a^2} + {b^2} + {c^2}\)

- Cho \(a = 30cm, b = 16cm,\) ta có:

\({a^2} + {b^2} + {c^2} = {50^2} \)

\(  \Rightarrow {30^2} + {16^2} + {c^2} = {50^2} \)

\(  \Rightarrow {c^2} = 2500 - 900 - 256 = 1344\)

\(  \Rightarrow c = \sqrt {1344}  \approx 36,7(cm)\)

Vậy các kích thước của hình hộp chữ nhật này là: \(a=30cm,b=16cm,c \approx 36,7cm\)

- Cho \(a = 25cm, b = 20cm,\) ta có:

\({a^2} + {b^2} + {c^2} = {50^2} \)

\(  \Rightarrow {25^2} + {20^2} + {c^2} = {50^2} \)

\(  \Rightarrow {c^2} = 2500 - 625 - 400 = 1475\)

\(  \Rightarrow c = \sqrt {1475}  \approx 38,4(cm)\)

Vậy các kích thước của hình hộp chữ nhật này là: \(a=25cm,b=20cm,c \approx 38,4cm\)