Bài 7* trang 37 SBT toán 7 tập 2
Giải bài 7* trang 37 sách bài tập toán 7. Cho tam giác ABC có AB < AC. Gọi M là trung điểm của BC. So sánh góc BAM và CAM.
Đề bài
Cho tam giác \(ABC\) có \(AB < AC.\) Gọi \(M\) là trung điểm của \(BC.\) So sánh \(\widehat {BAM}\) và \(\widehat {MAC}\).
Phương pháp giải - Xem chi tiết
Trên tia đối tia \(MA\) lấy điểm \(D\) sao cho \(MD = MA.\)
Sử dụng:
+) Tính chất hai tam giác bằng nhau
+) Trong một tam giác, đối diện với cạnh lớn hơn là góc lớn hơn.
Lời giải chi tiết
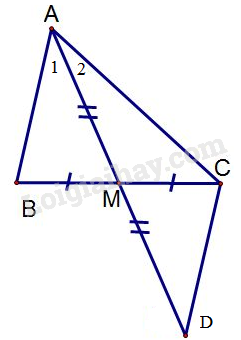
Trên tia đối tia \(MA\) lấy điểm \(D\) sao cho \(MD = MA.\)
Xét \(∆AMB\) và \(∆DMC\) ta có:
+) \(MA = MD\) (theo cách vẽ)
+) \(\widehat {AMB} = \widehat {DMC}\) (đối đỉnh)
+) \(MB = MC\) (vì M là trung điểm của BC)
Do đó: \(∆AMB = ∆DMC\) (c.g.c)
Nên: \(AB = CD\) (2 cạnh tương ứng)
Và \(\widehat D = \widehat {{A_1}}\) (2 góc tương ứng) (1)
Mà \(AB < AC\) (gt)
Suy ra: \(CD < AC\)
Trong \(∆ADC\) ta có: \(CD < AC\)
Nên \(\widehat D > \widehat {{A_2}}\) (góc đối diện cạnh lớn hơn là góc lớn hơn) (2)
Từ (1) và (2) suy ra: \(\widehat {{A_1}} > \widehat {{A_2}}\) hay \(\widehat {BAM} > \widehat {MAC}\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 7* trang 37 SBT toán 7 tập 2 timdapan.com"







