Bài 6 trang 37 SBT toán 7 tập 2
Giải bài 6 trang 37 sách bài tập toán 7. Cho tam giác ABC vuông tại A, tia phân giác của góc B cắt AC ở D. So sánh các độ dài AD, DC.
Đề bài
Cho tam giác \(ABC\) vuông tại \(A,\) tia phân giác của góc \(B\) cắt \(AC\) ở \(D.\) So sánh các độ dài \(AD, DC.\)
Phương pháp giải - Xem chi tiết
+) Kẻ \(DH \bot BC\) tại \(H\)
+) Sử dụng: Tính chất hai tam giác bằng nhau để chỉ ra \(AD=DH\)
+) Sử dụng: Trong tam giác vuông, cạnh huyền là cạnh lớn nhất.
Lời giải chi tiết
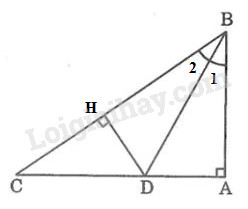
Kẻ \(DH \bot BC\) tại \(H\)
Xét hai tam giác vuông \(ABD\) và \(HBD:\)
+) \(\widehat {{B_1}} = \widehat {{B_2}}\) (vì BD là tia phân giác của góc ABC).
+) Cạnh huyền \(BD\) chung.
Do đó: \(∆ABD = ∆HBD\) (cạnh huyền - góc nhọn)
\( \Rightarrow AD = HD\) (2 cạnh tương ứng) (1)
Trong tam giác vuông \(DHC\) có \(\widehat {DHC} = 90^\circ \)
\( \Rightarrow DH < DC\) (cạnh góc vuông nhỏ hơn cạnh huyền) (2)
Từ (1) và (2) suy ra: \(AD < DC\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 6 trang 37 SBT toán 7 tập 2 timdapan.com"







