Bài 3 trang 36 SBT toán 7 tập 2
Giải bài 3 trang 36 sách bài tập toán 7. Cho tam giác ABC có góc B > 90 độ, điểm D nằm giữa B và C. Chứng minh rằng AB < AD < AC.
Đề bài
Cho tam giác ABC có \(\widehat B > 90^\circ \), điểm \(D\) nằm giữa \(B\) và \(C.\) Chứng minh rằng \(AB < AD < AC\)
Phương pháp giải - Xem chi tiết
Sử dụng:
+) Trong tam giác tù, góc tù là góc lớn nhất.
+) Trong một tam giác, góc ngoài tại một đỉnh lớn hơn góc trong không kề với đỉnh đó.
+) Trong tam giác, đối diện với góc lớn hơn là cạnh lớn hơn.
Lời giải chi tiết
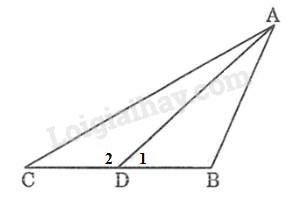
Trong \(∆ABC\) ta có: \(\widehat B > 90^\circ \)
\( \Rightarrow \widehat B > {\widehat D_1}\) (trong tam giác tù thì góc tù là góc lớn nhất)
Nên \(AD > AB\) (cạnh đối diện góc lớn hơn là cạnh lớn hơn) (1)
Trong \(∆ADC\) ta có \(\widehat {{D_2}}\) là góc ngoài tại đỉnh \(D\) của tam giác \(ABD\) nên \(\widehat {{D_2}} = \widehat B+\widehat {DAB}\), suy ra \(\widehat {{D_2}} > \widehat B > 90^\circ \)
Trong \(∆ADC\) ta có: \(\widehat {{D_2}} > 90^\circ \Rightarrow \widehat {{D_2}} > \widehat C\)
Nên \(AC > AD\) (đối diện góc lớn hơn là cạnh lớn hơn) (2)
Từ (1) và (2) suy ra: \(AB < AD < AC.\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 3 trang 36 SBT toán 7 tập 2 timdapan.com"







