Bài 63 trang 62 SBT toán 9 tập 2

Đề bài

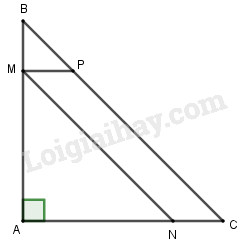
Cho tam giác \(ABC\) vuông cân có \(AB = AC = 12cm\). Điểm \(M \) chạy trên \(AB\). Tứ giác \(MNCP\) là một hình bình hành có đỉnh \(N \) thuộc cạnh \(AC \) (h.6). Hỏi khi \(M \) cách \(A \) bao nhiêu thì diện tích của hình bình hành bằng \(32cm^2\) ? 

Lời giải chi tiết

Gọi độ dài đoạn \(MA = x (cm)\); điều kiện \( 0 < x < 12\)

Vì \(∆ ABC\) vuông cân tại \(A\) nên tam giác \(BMP \) vuông cân tại \(M\)

\(⇒ MP = MB = AB – AM = 12 – x (cm)\)

Diện tích hình bình hành \(MNCP\) bằng \(MP.MA\)

Suy ra: \(MP.MA = (12 – x)x\)

Ta có phương trình:

\(\eqalign{
& \left( {12 - x} \right)x = 32 \cr 
& \Rightarrow {x^2} - 12x + 32 = 0 \cr 
& \Delta ' = {\left( { - 6} \right)^2} - 1.32 = 36 - 32 = 4 > 0 \cr 
& \sqrt {\Delta '} = \sqrt 4 = 2 \cr 
& {x_1} = {{6 + 2} \over 1} = 8 \cr 
& {x_2} = {{6 - 2} \over 1} = 4 \cr} \)

Cả hai giá trị \(x_1 = 8\) và \(x_2 = 4 \) thỏa mãn điều kiện bài toán 

Vậy điểm \(M\) cách điểm \(A\) là \(8cm\) hoặc \(4cm\) thì diện tích hình bình hành \(MNCP\) bằng \(32cm^2.\)