Bài 59 trang 48 SBT toán 7 tập 2
Giải bài 59 trang 48 sách bài tập toán 7. Cho hai điểm A, B và một đường thẳng d. Vẽ đường tròn tâm O đi qua hai điểm A, B sao cho O nằm trên đường thẳng d.
Đề bài
Cho hai điểm \(A, B\) và một đường thẳng \(d.\) Vẽ đường tròn tâm \(O\) đi qua hai điểm \(A, B\) sao cho \(O\) nằm trên đường thẳng \(d.\)
Phương pháp giải - Xem chi tiết
Sử dụng: Điểm cách đều hai mút của một đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó.
Lời giải chi tiết
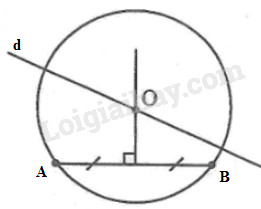
Phân tích:
Đường tròn tâm \(O\) đi qua hai điểm \(A\) và \(B.\)
Suy ra \(OA = OB\) nên \(O\) thuộc đường trung trực của đoạn \(AB.\)
Tâm \(O\) nằm trên đường thẳng \(d.\) Vậy tâm \(O\) là giao điểm của đường trung trực của \(AB\) và đường thẳng \(d.\)
Cách dựng:
- Dựng đường thẳng \(m\) là đường trung trực của \(AB\) cắt \(d\) tại \(O.\)
- Vẽ đường tròn tâm \(O\) bán kính \(OA\) (hoặc \(OB).\)
(Chú ý nếu \(m // d\) thì không dựng được tâm \(O,\) nếu \(m\) trùng với \(d\) thì có vô số điểm chung \(O\) do đó có vô số đường tròn thỏa mãn).
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 59 trang 48 SBT toán 7 tập 2 timdapan.com"







