Bài 56 trang 47 SBT toán 7 tập 2
Giải bài 56 trang 47 sách bài tập toán 7. Cho đường thẳng d và hai điểm A, B thuộc cùng một nửa mặt phẳng có bờ d. Tìm một điểm C nằm trên d sao cho C cách đều A và B.
Đề bài
Cho đường thẳng \(d\) và hai điểm \(A, B\) thuộc cùng một nửa mặt phẳng có bờ \(d.\) Tìm một điểm \(C \) nằm trên \(d\) sao cho \(C\) cách đều \(A\) và \(B.\)
Phương pháp giải - Xem chi tiết
Sử dụng: Điểm cách đều hai mút của một đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó
Lời giải chi tiết
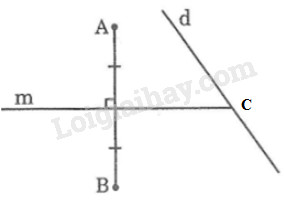
a) Nếu \(AB\) không vuông góc với \(d.\)
- Điểm \(C\) cách đều hai điểm \(A\) và \(B\) nên điểm \(C\) nằm trên đường trung trực của \(AB\)
- Điểm \(C ∈ d.\)
Vậy \(C\) là giao điểm của đường trung trực của \(AB\) và đường thẳng \(d.\)
Vẽ đường thẳng \(m\) là đường trung trực của đoạn thẳng \(AB\) cắt đường thẳng \(d\) tại \(C.\) Điểm \(C\) là điểm cần tìm.
b) Nếu \(AB \bot d\) thì đường trung trực của \(AB\) song song với đường thẳng \(d\) nên không tồn tại điểm \(C.\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 56 trang 47 SBT toán 7 tập 2 timdapan.com"







