Bài 50 trang 146 SBT toán 8 tập 2

Đề bài

Một nhà kho có dạng một lăng trụ đứng như hình 139 với \(BC = ED = CD = 10 \;(m)\) và \(DH = 20\; (m), AB = AE.\) Chiều cao từ đỉnh \(A\) đến nền nhà là \(15\; (m).\)

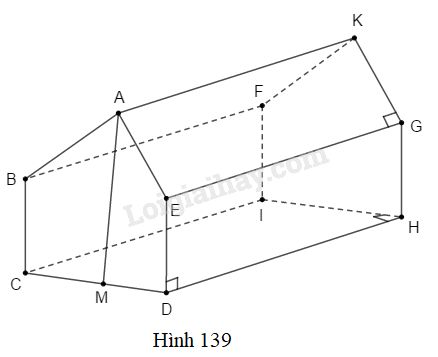
Thể tích nhà kho là \((m^3)\)

A. \(1800\)                                        B. \(2000\)

C. \(2500\)                                        D. \(2200\)

E. \(1600\)

Hãy chọn kết quả đúng.

Lời giải chi tiết

Chia nhà kho thành hai phần gồm lăng trụ đứng đáy hình tam giác cân \(ABE.KFG\) có cạnh đáy \(BE = CD = 10m,\) đường cao đáy bằng \(AM - BC = 15 - 10 = 5m\), đường cao lăng trụ là \(20m \) và hình hộp chữ nhật với đáy có kích thước \(10m\) và \(20m\), chiều cao bằng \(10m.\)

Thể tích lăng trụ tam giác là: \(\displaystyle V = S.h = {1 \over 2}.10.5.20 = 500\;({m^3})\)

Thể tích của hình hộp chữ nhật là: \(V = 10.20.10 = 2000\;({m^3})\)

Thể tích của kho là: \(500 + 2000 = 2500\;({m^3})\)

Chọn C.