Bài 41 trang 173 SBT toán 9 tập 2

Đề bài

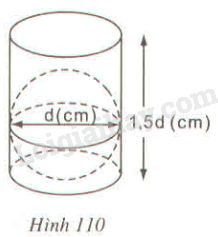
Một hình cầu đường kính \(d (cm) \) được đặt vào trong một hình trụ có chiều cao là \(1,5d (cm)\) như hình 110. Xét các phân số sau đây:

(A) \(\displaystyle{2 \over 3}\)                                (C) \(\displaystyle {2 \over 9}\)

(B) \(\displaystyle {4 \over 9}\)                                (D) \(\displaystyle {1 \over 3}\)

Đâu là tỉ số \(\displaystyle {{{V _\text{cầu}}} \over {{V _\text{trụ}}}}\)?

Lời giải chi tiết

Gọi \(r\) là bán kính đường tròn đáy hình trụ thì \(r\) cũng là bán kính hình cầu. 

Suy ra \(d=2r\)

Chiều cao hình trụ là: \(h = 1,5d = \dfrac{3}{2}d = \dfrac{3}{2}.2r = 3r\)

Thể tích của hình trụ là: \({V_1} = \pi {r^2}.h = \pi {r^2}.3r = 3\pi {r^3}\)

Thể tích của hình cầu là: \(\displaystyle {V_2} = {4 \over 3}\pi {r^3}\)

Ta có: \(\dfrac{{{V_2}}}{{{V_1}}} = \dfrac{{\dfrac{4}{3}\pi {r^3}}}{{3\pi {r^3}}} = \dfrac{4}{9}\).

Chọn (B).