Bài 33 trang 171 SBT toán 9 tập 2

Đề bài

Một quả bóng hình cầu bên trong một hình lập phương như hình 106.

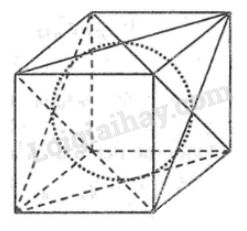
a) Tính tỉ số giữa diện tích toàn phần của hình lập phương với diện tích mặt cầu

b) Nếu diện tích mặt cầu là \(7\pi (c{m^2})\) thì diện tích toàn phần của hình lập phương là bao nhiêu?

c) Nếu bán kính hình cầu là \(4cm\) thì thể tích phần trống (trong hình hộp ngoài hình cầu) là bao nhiêu?

Lời giải chi tiết

Gọi cạnh hình lập phương là \(a\) thì bán kính cầu \(\displaystyle r = {a \over 2}\).

a) Diện tích toàn phần của hình lập phương là: \({S_1} = 6{a^2}\) (đơn vị diện tích)

Diện tích mặt cầu là: \(\displaystyle {S_2} = 4.\pi .{\left( {{a \over 2}} \right)^2} = 4\pi .{{{a^2}} \over 4} = \pi {a^2}\) (đơn vị diện tích)

Tỉ số \(\dfrac{{{S_1}}}{{{S_2}}} = \dfrac{{6{a^2}}}{{\pi {a^2}}} = \dfrac{6}{\pi }\)

b) Theo câu a ta có \(\dfrac{{{S_1}}}{{{S_2}}}  = \dfrac{6}{\pi }\)

Diện tích mặt cầu bằng \(7\pi (c{m^2})\) nên ta có \(\displaystyle  \dfrac{{{S_1}}}{{7\pi }}= {6 \over \pi }\)

\( \displaystyle  \Rightarrow {S_1} = {6 \over \pi }.7\pi  = 42\) \(\left( {c{m^2}} \right)\)

Vậy diện tích mặt cầu là \(7\pi (c{m^2})\) thì diện tích toàn phần của hình lập phương là \(42\) \(\left( {c{m^2}} \right)\).

c) Bán kính hình cầu \(r = 4cm\) thì cạnh hình lập phương \(a=2r = 8cm\).

Thể tích của hình lập phương là: \({V_1} = {a^3} = {8^3} = 512\left( {c{m^3}} \right)\)

Thể tích hình cầu là: \(\displaystyle  {V_2} = {4 \over 3}\pi {r^3} = {4 \over 3}\pi {.4^3} = {{256} \over 3}\pi \left( {c{m^3}} \right)\)

Thể tích hình lập phương nằm ngoài hình cầu là:

\(V = {V_1} - {V_2} =\displaystyle   512 - {{256} \over 3}\pi\)\(\,  \approx 243,917\left( {c{m^3}} \right)\)