Bài 3.9 trang 104 SBT hình học 12

Đề bài

Trong không gian Oxyz cho một vecto \(\overrightarrow a \) tùy ý khác vecto \(\overrightarrow 0 \). Gọi \(\alpha ,\beta ,\gamma \) là ba góc tạo bởi ba vecto đơn vị \(\overrightarrow i ,\overrightarrow j ,\overrightarrow k \) trên ba trục Ox, Oy, Oz và vecto \(\overrightarrow a \). Chứng minh rằng:  \({\cos ^2}\alpha  + {\cos ^2}\beta  + {\cos ^2}\gamma  = 1\)

Lời giải chi tiết

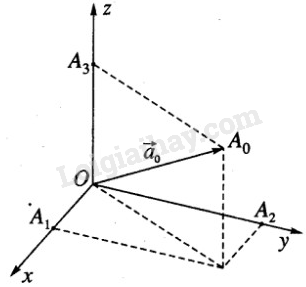
Gọi \(\overrightarrow {{a_0}} \) là vecto đơn vị cùng hướng với vecto \(\overrightarrow a \), ta có \(\overrightarrow {{a_0}}  = \dfrac{1}{{|\overrightarrow a |}}\overrightarrow a \).

Gọi \(\overrightarrow {O{A_0}}  = \overrightarrow {{a_0}} \) và các điểm A₁, A₂, A₃ theo thứ tự là hình chiếu vuông góc của điểm A₀ trên các trục Ox, Oy, Oz.

Khi đó ta có:  \(\) \(\dfrac{{|\overrightarrow {O{A_1}} |}}{{|\overrightarrow {O{A_0}} |}} = \cos \alpha ,\dfrac{{|\overrightarrow {O{A_2}} |}}{{|\overrightarrow {O{A_0}|} }} = \cos \beta ,\dfrac{{|\overrightarrow {O{A_3}} |}}{{|\overrightarrow {O{A_0}} |}} = \cos \gamma \)

Vì  \(|\overrightarrow {O{A_0}} | = 1\) nên  \(|\overrightarrow {O{A_1}} | = \cos \alpha ,|\overrightarrow {O{A_2}} | = \cos \beta ,|\overrightarrow {O{A_3}} | = \cos \gamma \)

Ta có \(\overrightarrow {O{A_0}}  = \overrightarrow {O{A_1}}  + \overrightarrow {O{A_2}}  + \overrightarrow {O{A_3}} \)  , ta suy ra:  \(\overrightarrow {O{A_0}}  = \cos \alpha \overrightarrow i  + \cos \beta \overrightarrow j  + \cos \gamma \overrightarrow k \) hay  \(\overrightarrow {O{A_0}}  = (\cos \alpha ;\cos \beta ;\cos \gamma )\).

Vì  \(\overrightarrow {O{A_0}}  = \overrightarrow {{a_0}} \)  mà \(|\overrightarrow {{a_0}} | = 1\) nên ta có: \({\cos ^2}\alpha  + {\cos ^2}\beta  + {\cos ^2}\gamma  = 1\)