Bài 3.62 trang 134 SBT hình học 12

Đề bài

Cho hình lập phương ABCD.A₁B₁C₁D₁ có cạnh bằng 1. Gọi M, N, P lần lượt là trung điểm của các cạnh BB₁, CD, A₁D₁. Tính khoảng cách và góc giữa hai đường thẳng MP và C₁N.

Lời giải chi tiết

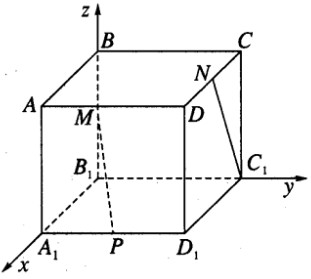
Ta chọn hệ trục tọa độ như sau:  B₁ là gốc tọa độ, \(\overrightarrow {{B_1}{A_1}}  = \overrightarrow i ,\overrightarrow {{B_1}{C_1}}  = \overrightarrow j ,\overrightarrow {{B_1}B}  = \overrightarrow k \).

Trong hệ trục vừa chọn, ta có B₁(0; 0; 0), B(0; 0; 1), A₁(1; 0; 0), D₁(1; 1; 0), C(0; 1; 1), D(1; 1; 1), C₁(0; 1; 0).

Suy ra \(M\left( {0;0;\dfrac{1}{2}} \right),P\left( {1;\dfrac{1}{2};0} \right),N\left( {\dfrac{1}{2};1;1} \right)\)

Ta có \(\overrightarrow {MP}  = \left( {1;\dfrac{1}{2}; - \dfrac{1}{2}} \right);\)\(\overrightarrow {{C_1}N}  = \left( {\dfrac{1}{2};0;1} \right)\)

Gọi \((\alpha )\) là mặt phẳng chứa \(C_1N\) và song song với MP.

\( \Rightarrow \overrightarrow {{n_\alpha }}  = \left[ {\overrightarrow {MP} ,\overrightarrow {{C_1}N} } \right] = \left( {\dfrac{1}{2}; - \dfrac{5}{4}; - \dfrac{1}{4}} \right)\) hay chọn \(\overrightarrow n = (2; - 5; - 1)\) là VTPT của \((\alpha)\)

Phương trình  của \((\alpha )\) là   \(2x – 5(y – 1) – z = 0 \) hay \(2x – 5y – z + 5 = 0\)

Ta có  \(d(MP,{C_1}N) = d(M,(\alpha )) \) \(= \dfrac{{| - \dfrac{1}{2} + 5|}}{{\sqrt {25 + 4 + 1} }} = \dfrac{9}{{2\sqrt {30} }}\)

Ta có:  \(\cos ({MP,{C_1}N}) = \dfrac{{|\overrightarrow {MP} .\overrightarrow {{C_1}N} |}}{{|\overrightarrow {MP} |.|\overrightarrow {{C_1}N} |}} = 0\).  Vậy \((\widehat {MP,{C_1}N}) = {90^0}\)