Bài 32* trang 161 SBT toán 9 tập 1
Giải bài 32* trang 161 sách bài tập toán 9. Cho đường tròn tâm O bán kính 5dm, điểm M cách O là 3dm...
Đề bài
Cho đường tròn tâm \(O\) bán kính \(5dm,\) điểm \(M\) cách \(O\) là \(3dm.\)
\(a)\) Tính độ dài dây ngắn nhất đi qua điểm \(M.\)
\(b)\) Tính độ dài dây dài nhất đi qua \(M.\)
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức:
+) Trong các dây của một đường tròn, dây lớn nhất là đường kính.
+) Trong hai dây của đường trond, dây nào lớn hơn thì dây đó gần tâm hơn.
Lời giải chi tiết
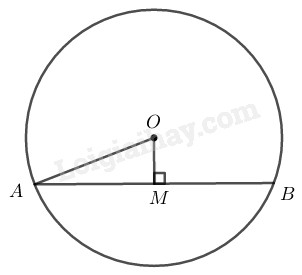
\(a)\) Dây đi qua \(M\) ngắn dây là dây \(AB\) vuông góc với \(OM.\)
Áp dụng định lí Pi-ta-go vào tam giác vuông \(OAM\) ta có:
\(O{A^2} = A{M^2} + O{M^2}\)
Suy ra: \(A{M^2} = O{A^2} - O{M^2} = {5^2} - {3^2} = 16\)
\(AM = 4 (dm)\)
Ta có: \( OM ⊥ AB\)
Suy ra: \( AM = \displaystyle {1 \over 2}AB\)
Hay: \( AB = 2AM = 2.4 = 8 (dm)\)
\(b)\) Dây đi qua \(M\) lớn nhất khi nó là đường kính của đường tròn \((O).\) Vậy dây có độ dài bằng \(2R = 2.5 = 10 (dm)\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 32* trang 161 SBT toán 9 tập 1 timdapan.com"







