Bài 25 trang 160 SBT toán 9 tập 1
Giải bài 25 trang 160 sách bài tâp toán 9. Cho hình 75, trong đó hai dây CD, EF bằng nhau và vuông góc với nhau tại I, IC = 2cm, ID = 14cm. Tính khoảng cách từ O đến mỗi dây.
Đề bài
Cho hình \(75,\) trong đó hai dây \(CD, EF\) bằng nhau và vuông góc với nhau tại \(I,\) \(IC = 2cm,\) \(ID = 14cm.\) Tính khoảng cách từ \(O\) đến mỗi dây.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức: Trong một đường tròn:
+) Hai dây bằng nhau thì cách đều tâm.
+) Đường kính vuông góc với một dây không đi qua tâm thì đi qua trung điểm của dây ấy.
Lời giải chi tiết
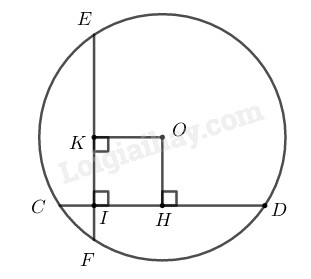
Kẻ \(OH ⊥ CD,\) \(OK ⊥EF\)
Vì tứ giác \(OKIH\) có ba góc vuông nên nó là hình chữ nhật.
Ta có: \(CD = EF\;\; (gt)\)
Suy ra: \(OH = OK\) (hai dây bằng nhau cách đều tâm)
Suy ra tứ giác \(OKIH\) là hình vuông.
Ta có:\(CD = CI + ID = 2 + 14 =16\; (cm)\)
\(HC = HD = \displaystyle {{CD} \over 2} = 8\) \((cm)\) (quan hệ giữa đường kính và dây cung)
\(IH = HC – CI = 8 – 2 = 6\; (cm)\)
Suy ra: \(OH = OK = 6\; (cm)\) (\(OKIH\) là hình vuông).
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 25 trang 160 SBT toán 9 tập 1 timdapan.com"







