Bài 26 trang 160 SBT toán 9 tập 1
Giải bài 26 trang 160 sách bài tập toán 9. Cho đường tròn (O), dây AB và dây CD, AB < CD. Giao điểm K của các đường thẳng AB, CD nằm ngoài đường tròn. Đường tròn (O ; OK) cắt KA và KC tại M và N. Chứng minh rằng KM < KN.
Đề bài
Cho đường tròn \((O),\) dây \(AB\) và dây \(CD,\) \(AB < CD.\) Giao điểm \(K\) của các đường thẳng \(AB,\) \(CD\) nằm ngoài đường tròn. Đường tròn \((O ; OK)\) cắt \(KA\) và \(KC\) tại \(M\) và \(N.\) Chứng minh rằng \(KM < KN.\)
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức: Trong hai dây của một đường tròn:
+) Dây nào lớn hơn thì dây đó gần tâm hơn.
+) Dây nào gần tâm hơn thì dây đó lớn hơn.
Lời giải chi tiết
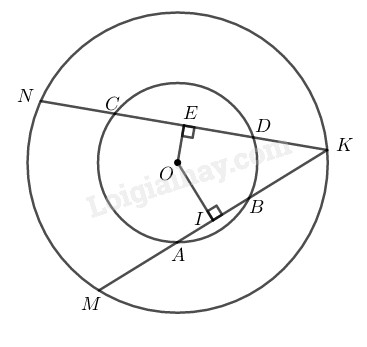
Kẻ \(OI ⊥ AB,\) \(OE ⊥ CD\)
Trong \(( O ; OA)\) ta có: \(AB < CD\;\; (gt)\)
Suy ra: \(OI > OE\) (dây lớn hơn gần tâm hơn)
Trong \((O ; OK)\) ta có: \(OI > OE \) (cmt)
Suy ra: \(KM < KN \) (dây gần tâm hơn thì lớn hơn).
Mẹo Tìm đáp án nhanh nhất
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 26 trang 160 SBT toán 9 tập 1 timdapan.com"
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 26 trang 160 SBT toán 9 tập 1 timdapan.com"







