Bài 27 trang 160 SBT toán 9 tập 1
Giải bài 27 trang 160 sách bài tập toán 9. Cho đường tròn (O) và điểm I nằm bên trong đường tròn. Chứng minh rằng dây AB vuông góc với OI tại I ngắn hơn mọi dây khác đi qua I.
Đề bài
Cho đường tròn \((O)\) và điểm \(I\) nằm bên trong đường tròn. Chứng minh rằng dây \(AB\) vuông góc với \(OI\) tại \(I\) ngắn hơn mọi dây khác đi qua \(I.\)
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức: Trong hai dây của một đường tròn:
+) Dây nào lớn hơn thì dây đó gần tâm hơn.
Lời giải chi tiết
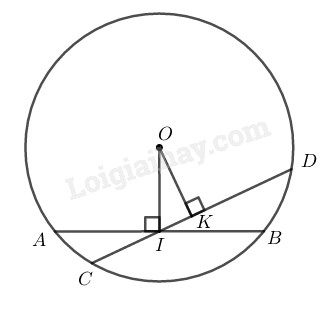
Gọi \(CD\) là dây bất kì đi qua \(I\) và \(CD\) không vuông góc với \(OI.\)
Kẻ \(OK ⊥ CD\)
Tam giác \(OKI\) vuông tại \(K\) nên \(OI > OK\)
Suy ra: \(AB < CD\) ( dây lớn hơn gần tâm hơn)
Vậy dây \(AB\) vuông góc với \(IO\) tại \(I\) ngắn hơn mọi dây khác đi qua \(I.\)
Mẹo Tìm đáp án nhanh nhất
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 27 trang 160 SBT toán 9 tập 1 timdapan.com"
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 27 trang 160 SBT toán 9 tập 1 timdapan.com"







