Bài 2.1 phần bài tập bổ sung trang 159 SBT toán 9 tập 1

Đề bài

Độ dài cạnh của tam giác đều nội tiếp đường tròn \((O; R)\) bằng: 

(A) \(\dfrac{R}{2}\) ;                      (B) \(\dfrac{{R\sqrt 3 }}{ 2}\) ;

(C) \(R\sqrt 3 \) ;                   (D) Một đáp số khác.

Hãy chọn phương án đúng.

Lời giải chi tiết

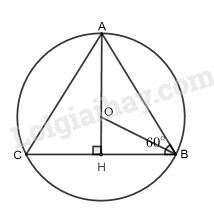
Tam giác \(ABC\) đều nên tia \(OB\) là tia phân giác góc \(ABH\), suy ra \(\widehat {OBH} = 30^\circ \)

Xét tam giác \(OBH\) 

\(BH = OB.c{\rm{os30}}^\circ {\rm{ = }}\dfrac{{\sqrt 3 }}{2}R\)

Vây \(CB = 2.BH = 2.\dfrac{{\sqrt 3 }}{2}R = \sqrt 3 R\)

Vậy đáp án là (C).