Bài 19 trang 73 Vở bài tập toán 7 tập 2

Đề bài

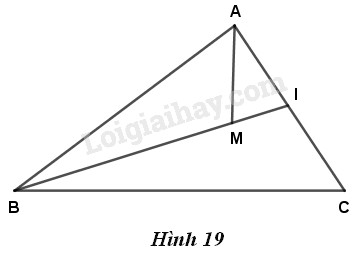
Cho tam giác \(ABC\) và \(M\) là một điểm nằm trong tam giác. Gọi \(I\) là giao điểm của đường thẳng \(BM\) và cạnh \(AC\) (h.19).

a) So sánh \(MA\) với \(MI + IA\), từ đó chứng minh \(MA + MB < IB + IA.\)

b) So sánh \(IB\) với \(IC + CB\), từ đó chứng minh \(IB + IA < CA + CB\).

c) Chứng minh bất đẳng thức \(MA + MB < CA + CB.\)

Lời giải chi tiết

a) Xét tam giác \(AMI\). Theo bất đẳng thức tam giác, ta có \(MA < MI + IA\).

Suy ra \(MA + MB < MI + IA+MB\), hay \(MA + MB < IB + IA\) (1).

b) Áp dụng bất đẳng thức tam giác vào tam giác \(IBC\), ta có \(IB < IC + BC\).

Suy ra \(IB + IA < IC + BC+IA\) hay \(IB + IA < AC + BC\) (2).

c) Từ (1) và (2) suy ra \(MA + MB < CA + CB\).