Bài 19 trang 65 SBT toán 9 tập 1

Biết rằng với \(x = 4\) thì hàm số \(y = 2x + b\) có giá trị \(5.\)

LG a

Tìm \(b;\) 

Phương pháp giải:

Gọi d là đồ thị của hàm số  \(y = ax + b\) \((a \ne 0)\), \(d\) cắt trục hoành tại \(B\left( { - \dfrac{b}{a};0} \right)\) và cắt trục tung tại \(A\left( {0;b} \right)\).

Điểm \(M({x_0};{y_0})\) thuộc \(d\) khi và chỉ khi \(y_0 = ax_0 + b\).

Lời giải chi tiết:

Với \(x = 4\) thì hàm số \(y = 2x + b\) có giá trị là \(5\) , ta có:

\(5 = 2.4 + b \Leftrightarrow b = 5 - 8 \Leftrightarrow b =  - 3\)

LG b

Vẽ đồ thị của hàm số ứng với giá trị của b tìm được ở câu a). 

Phương pháp giải:

Gọi d là đồ thị của hàm số  \(y = ax + b\) \((a \ne 0)\), \(d\) cắt trục hoành tại \(B\left( { - \dfrac{b}{a};0} \right)\) và cắt trục tung tại \(A\left( {0;b} \right)\).

Điểm \(M({x_0};{y_0})\) thuộc \(d\) khi và chỉ khi \(y_0 = ax_0 + b\).

Lời giải chi tiết:

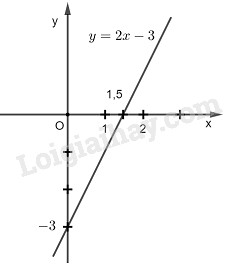
Vẽ đồ thị hàm số \(y = 2x - 3\)

Cho \(x = 0\) thì \(y = -3\) . Ta có : \(A(0;-3)\)

Cho \(y = 0\) thì \(x = 1,5.\) Ta có: \(B(1,5;0)\)

Đồ thị của hàm số \(y = 2x + 3\) là đường thẳng đi qua hai điểm \(A, B.\)