Bài 1.79 trang 40 SBT giải tích 12

Đề bài

Cho hàm số: \(y =  - {x^4} - {x^2} + 6\)

a) Khảo sát sự biến thiên và vẽ đồ thị \(\left( C \right)\) của hàm số đã cho.

b) Viết phương trình tiếp tuyến của đồ thị \(\left( C \right)\) biết tiếp tuyến vuông góc với đường thẳng:  \(y = \dfrac{1}{6}x - 1\)

(Đề thi tốt nghiếp THPT năm 2010)

LG câu a

Phương pháp:

Khảo sát tóm tắt:

- Tìm TXĐ.

- Lập bảng biến thiên.

- Vẽ đồ thị hàm số.

Cách giải:

TXĐ: \(D = \mathbb{R}\).

Chiều biến thiên:

Ta có: \(y' =  - 4{x^3} - 2x =  - 2x\left( {2{x^2} + 1} \right)\); \(y' = 0 \Leftrightarrow x = 0\).

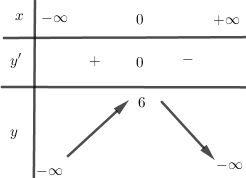
Hàm số nghịch biến trên \(\left( {0; + \infty } \right)\) và đồng biến trên \(\left( { - \infty ;0} \right)\).

Hàm số đạt cực đại tại \(x = 0\), \({y_{CD}} = 6\) và không có cực tiểu.

Bảng biến thiên:

Đồ thị:

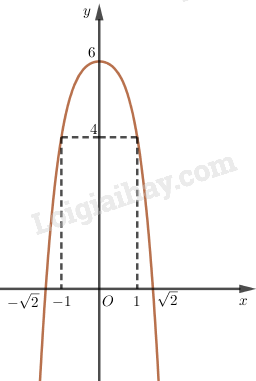
Đồ thị đi qua các điểm \(\left( {1;4} \right)\) và \(\left( { - 1;4} \right)\), cắt trục hoành tại hai điểm \(\left( { \pm \sqrt 2 ;0} \right)\).

LG câu b

Phương pháp:

- Tìm hệ số góc \(k\) của tiếp tuyến dựa vào lý thuyết: Hai đường thẳng vuông góc vơi nhau thì tích hệ số góc bằng \( - 1\).

- Giải phương trình \(y' = k\) tìm hoành độ tiếp điểm.

- Viết phương trình tiếp tuyến theo công thức \(y = k\left( {x - {x_0}} \right) + {y_0}\).

Cách giải:

Ta có: \(y' =  - 4{x^3} - 2x\)

Vì tiếp tuyến vuông góc với đường thẳng \(y = \dfrac{1}{6}x - 1\) nên tiếp tuyến có hệ số góc là \( - 6\).

Ta có: \( - 4{x^3} - 2x =  - 6\)\( \Leftrightarrow 2{x^3} + x - 3 = 0\)

\( \Leftrightarrow 2({x^3} - 1) + (x - 1) = 0\)\( \Leftrightarrow (x - 1)(2{x^2} + 2x + 3) = 0\) \( \Leftrightarrow x = 1\)  (vì \(2{x^2} + 2x + 3 > 0,\forall x\))

Suy ra \(y\left( 1 \right) = 4\).

Phương trình tiếp tuyến là: \(y =  - 6\left( {x - 1} \right) + 4\) hay \(y =  - 6x + 10\).