Bài 1.59 trang 24 SBT hình học 12

Đề bài

Cho khối lập phương \(ABCD.A'B'C'D'\) cạnh bằng \(a\). Gọi \(M,N\) lần lượt là trung điểm của các cạnh \(AB,AD\). Mặt phẳng \(\left( {MB'D'N} \right)\) chia khối lập phương đã cho thành hai khối đa diện. Gọi \(\left( H \right)\) là khối đa diện chứa đỉnh \(A\). Thể tích của khối đa diện \(\left( H \right)\) bằng:

A. \(\dfrac{{{a^3}}}{9}\)                B. \(\dfrac{{{a^3}}}{6}\)

C. \(\dfrac{{{a^3}}}{4}\)                D. \(\dfrac{{7{a^3}}}{{24}}\)

Lời giải chi tiết

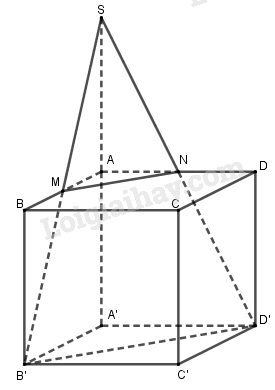
Kéo dài \(B'M,D'N\) cắt nhau tại \(S\).

Ta có: \(\left\{ \begin{array}{l}\left( {B'MND'} \right) \cap \left( {ABB'A'} \right) = B'M\\\left( {B'MND'} \right) \cap \left( {ADD'A'} \right) = D'N\\\left( {ABB'A'} \right) \cap \left( {ADD'A'} \right) = A'A\\B'M \cap D'N = \left\{ S \right\}\end{array} \right.\) \( \Rightarrow S \in A'A\).

Lại có \(\dfrac{{SA}}{{SA'}} = \dfrac{{SN}}{{SD'}} = \dfrac{{AN}}{{A'D'}} = \dfrac{1}{2}\)\( \Rightarrow SA = \dfrac{1}{2}SA'\) hay \(A\) là trung điểm của \(SA'\) hay \(SA = A'A = a\).

Ta có: \({V_{S.AMN}} = \dfrac{1}{3}SA.{S_{AMN}}\) \( = \dfrac{1}{3}a.\dfrac{1}{2}.\dfrac{a}{2}.\dfrac{a}{2} = \dfrac{{{a^3}}}{{24}}\).

\({V_{S.A'B'D'}} = \dfrac{1}{3}SA'.{S_{A'B'D'}}\) \( = \dfrac{1}{3}2a.\dfrac{1}{2}a.a = \dfrac{{{a^3}}}{3}\).

Vậy \({V_{AMN.A'B'D'}} = {V_{S.A'B'D'}} - {V_{S.AMN}}\) \( = \dfrac{{{a^3}}}{3} - \dfrac{{{a^3}}}{{24}} = \dfrac{{7{a^3}}}{{24}}\).

Chọn D.