Bài 1.53 trang 23 SBT hình học 12

Đề bài

Cho hình chóp \(S.ABC\) có \(SA\) vuông góc với đáy. Mặt phẳng qua \(A\) và vuông góc với \(SC\) cắt \(SB,SC\) lần lượt tại \(M,N\). Biết rằng \(SA = AC = 5\), \(AB = 3,BC = 4\). Thể tích khối chóp \(S.AMN\) bằng

A. \(\dfrac{{125}}{{68}}\)                     B. \(\dfrac{{125}}{{34}}\)

C. \(\dfrac{{175}}{{34}}\)                     D. \(\dfrac{{125}}{{17}}\)

Lời giải chi tiết

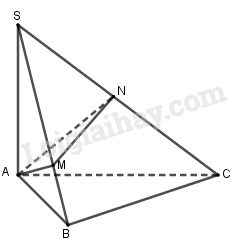
Ta có: \(SC \bot \left( {AMN} \right) \Rightarrow \left\{ \begin{array}{l}SC \bot AM\\SC \bot MN\end{array} \right.\).

Tam giác \(ABC\) có \(A{C^2} = A{B^2} + B{C^2}\) nên vuông tại \(B\).

Suy ra \(AB \bot BC\), mà \(SA \bot BC\) nên \(BC \bot \left( {SAB} \right) \Rightarrow BC \bot SB\).

Tam giác \(SMN\) đồng dạng tam giác \(SCB\) (g.g) \( \Rightarrow \dfrac{{{S_{SMN}}}}{{{S_{SCB}}}} = {\left( {\dfrac{{SN}}{{SB}}} \right)^2}\)

Tam giác \(SAC\) vuông cân tại \(A\) có \(AN \bot SC\) \( \Rightarrow SN = \dfrac{1}{2}SC = \dfrac{1}{2}\sqrt {{5^2} + {5^2}}  = \dfrac{{5\sqrt 2 }}{2}\).

Tam giác \(SAB\) có \(SA = 5,AB = 3 \Rightarrow SB = \sqrt {34} \)

\( \Rightarrow \dfrac{{{S_{SMN}}}}{{{S_{SCB}}}} = {\left( {\dfrac{{SN}}{{SB}}} \right)^2} = \dfrac{{25}}{{68}}\)\( \Rightarrow \dfrac{{{V_{S.AMN}}}}{{{V_{S.ABC}}}} = \dfrac{{25}}{{68}}\).

Mà \({V_{S.ABC}} = \dfrac{1}{3}SA.{S_{ABC}} = \dfrac{1}{3}.5.\dfrac{1}{2}.3.4 = 10\) nên \({V_{S.AMN}} = \dfrac{{25}}{{68}}.10 = \dfrac{{125}}{{34}}\).

Chọn B.